题目内容
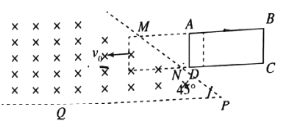
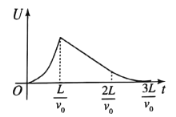
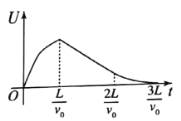
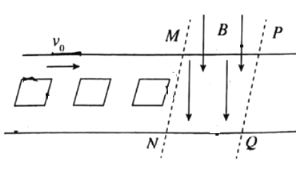
【题目】如图所示,水平传送带上放置n个相同的正方形闭合导线圈,每个线圈的质量均为m,电阻均为R,边长均为L,线框与传送带间的动摩擦因数均为μ,线圈与传送带共同以速度外匀速向右运动。MN与PQ为匀强磁场的边界,平行间距为d(L<d),速度v0方向与MN垂直。磁场的磁感应强度为B,方向竖直向下。当线圈右侧边进入磁场边界PQ时与传送带发生相对运动,线圈的右侧边经过边界时又恰好与传送带的速度相同。设传送带足够长, 且线框在传送带上始终保持右侧边平行于磁场边界。已知重力加速度为g,线圈间不会相碰。求:
(1)线圈的右侧边刚进入磁场时,线圈的加速度大小;
(2)线圈右侧边从MN运动到PQ经过的时间t;
(3)n个线圈均通过磁场区域到恢复和传送带共速,线圈释放的焦耳热。
【答案】(1)![]() -μg方向向左;(2)
-μg方向向左;(2)![]() ;(3)2nμmgd
;(3)2nμmgd
【解析】
(1)线圈刚进入磁场,由法拉第电磁感应定律:
E=BLv0
根据闭合电路欧姆定律:
I=![]()
所以安培力
F=![]()
根据牛顿第二定律:
F-μmg=ma.
所以
a=![]() -μg,方向向左
-μg,方向向左
(2 )根据动量定理,对线圈:
μmgt -I安=0.
其中安培力的冲量:
I安= F安t′=B![]() L·t′=BLq
L·t′=BLq
q=![]() .
.
综上解得
t=![]() .
.
(3)自线圈进入磁场到线圈右侧边界到达PQ过程中,根据动能定理
μmgd-W安=0.
所以克服安培力做功
W安=μmgd
线圈离开磁场的运动情况和进入磁场相同,
W安′=μmgd
所以
Q=2nμmgd

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目