题目内容
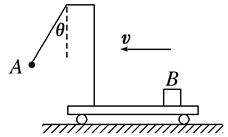
（15分）如图所示，竖直平面内的3/4圆弧形光滑轨道半径为R，A端与圆心O等高，AD为与水平方向成45°角的斜面，B端在O的正上方，一个小球在A点正上方由静止开始释放，自由下落至A点后进入圆形轨道并恰能到达B点.求：
（1）到达B点的速度大小?（2）释放点距A点的竖直高度;（3）小球落到斜面上C点时的速度大小和方向.
（1）
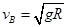（2）
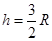（3）
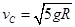,与水平方向夹角的正切值是2
解析试题分析：（1）小球到达B点：由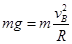
解得：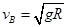
（2）设小球的释放点距A点高度为
，由机械能守恒定律得：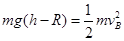
解得：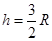
（3）小球落到C点时：由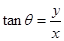
，得：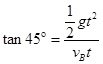
解得：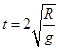
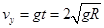
小球落到C点得速度大小：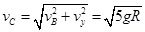
小球落到C点时，速度与水平方向夹角为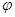
：
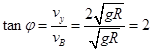
考点：本题考查了牛顿第二定律、机械能守恒定律、平抛运动.
练习册系列答案
相关题目
的物体，让其在随位移均匀减小的水平推力作用下运动，推力
随位移
变化的图象如图乙所示。已知物体与地面之间的动摩擦因数为
，
.求：
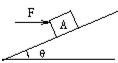
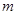的小球，以初速度
沿轨道向上运动，求：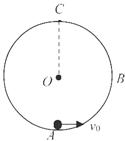
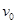大小可调节，小球在运动过程中出现脱轨现象，则
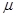）。某时刻观察到细线偏离竖直方向
角，