Question

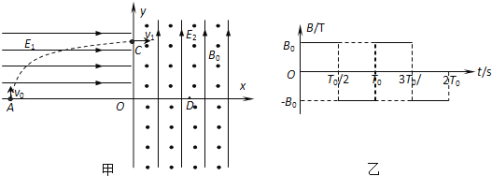
【题目】如图，两个水平宽度均为d＝0.2m的相邻区域Ⅰ、Ⅱ存在磁场和电场，其中区域Ⅰ有匀强磁场，方向垂直纸面向外，磁感应强度B=0.1T，区域Ⅱ有水平向左的匀强电场E。某带正电微粒从区域Ⅰ的左侧某点射入磁场，入射速度大小v=103m/s，与水平方向成30°。已知微粒的比荷，不计重力。

(1)为了使微粒不从Ⅱ区域的右侧射出电场，匀强电场的电场强度E至少为多大；

(2)现将区域Ⅰ的磁感应强度改变为B'=0.2T，通过调节E的大小，微粒在整个场区运动的时间不同，求微粒从进入到射出场区的最长时间。（结果用根式表示）

Answer 1

【答案】(1)E=1.0×102V/m；(2)

【解析】

(1)粒子在磁场中做圆周运动，有

得：

代入数据解得：

由题知d＝0.2m则

由几何关系得，粒子在磁场中圆运动的圆心在磁场的右边界线，粒子平行于电场射入电场，粒子运动轨迹如图所示

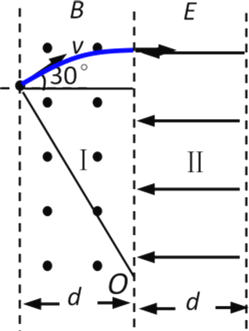
粒子进入电场时，初速度大小为v，粒子在电场中向右做匀减速直线运动，要使粒子不射出电场，粒子在电场中运动距离应小于d，考虑临界，由动能定理有

解得：

代入数据得：

(2)当将磁感应强度变为B'时，有

代入数据得，微粒的运动半径为

由几何关系得，微粒运动的圆心恰好在磁场区域的正中间，微粒在磁场中出射点与入射点在同一水平线，且出射速度方向与水平方向夹角为，粒子进入电场做类斜抛运动，经分析知，粒子在场区运动的最长时间即粒子轨迹恰好与电场右边界相切，如图所示

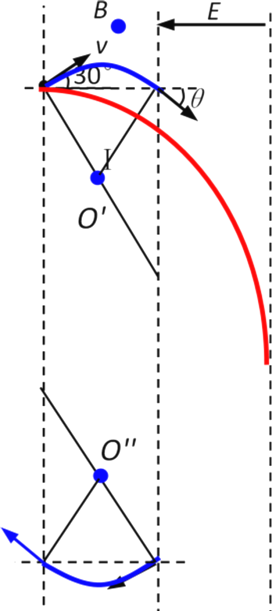
从粒子进入磁场到射入电场运动时间

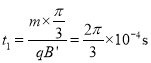
粒子在电场中运动总时间为t2，考虑类斜抛轨迹对称，在水平方向有

解得：

由对称性知，粒子第二次在磁场中运动的时间

粒子在整个场区运动的最长时间

代入数据得：