题目内容
【题目】如图，在xoy坐标中存在一方向垂直于纸面、磁感应强度为B的有界磁场磁场宽度x＝1．有一质量为m的带电粒子q无初速地从A点处进入加速电场，经加速度后垂直y轴且从y＝2处进入磁场，再经磁场偏转后从边界C点射出，最后打在x轴的P点上，CP与x轴的夹角为60°．不计粒子的重力，求：
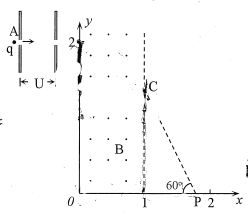
（1）加速电场的电压U
（2）带电粒子在磁场中的运动时间t
（3）P点在x轴上的坐标xp。
【答案】（1）
（2）
（3）
【解析】
做出带电粒子在磁场中的运动轨迹，由几何知识求出半径，根据洛伦兹力提供向心力求出速度，在电场中根据动能定理列方程求加速电场的电压；
找到圆周运动轨迹所对的圆心角分析求解粒子在磁场中运动的时间，根据几何知识求解P点的横坐标；
（1）设粒子在磁场中运动的速度为v，运动半径为r，则
对加速电场有：qU=
mv2，
在磁场中偏转有：
粒子在磁场中的运动轨迹如图所示，
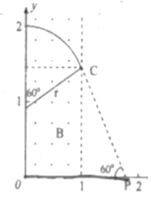
根据几何关系可知：rsin60°＝l，
由以上式子联立解得： ；
（2）粒子周期为
，
粒子在磁场中的运动时间为
；
（3）根据几何知识可知，P点在x轴上的坐标为
；
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
