题目内容
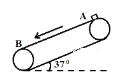
【题目】如图所示，倾角为
的斜面上静置一质量为
的薄木板，木板的长度为
，质量
的物块（可视为质点）以初速度
沿木板顶端运动，物块与木板之间的动摩擦因数
，木板与斜面之间的动摩擦因数
，斜面的底端固定一垂直于斜面的挡板，木板的下端距离挡板为
，木板与挡板碰撞后立即粘在一起停止运动。设物块与木板之间、木板与斜面之间的动摩擦力等于最大静摩擦力，则（重力加速度
)
(1)物块落到斜面上后，木板经过多长时间与挡板相碰；
(2)木板与挡板碰前的速度；
(3)物块总共发生的位移。
【答案】(1)7s；(2)
；(3)
【解析】
(1)(2)取沿斜面向下为正方向，对物块，由牛顿第二定律得
可得
即物块做匀减速直线运动
对木板，由牛顿第二定律得
解得
即木板向下做初速度为0的匀加速直线运动
若木板一直加速运动与挡板相碰，设所需加时间为
，由运动学公式则有
解得
若木板与物块先共速再与挡板相碰，设经
共速，由运动学公式则有
解得
由于
，故木板先与物块共速再与挡板相碰，共同速度为
木板匀加速位移
物块，与木板共速前的减速位移为
物块相对于木位移
故共速时，物块还未滑至低端
由于
，故木块和物块共速后匀速，木板与物块匀速时间
物块落上木板到木板与挡板碰撞时间
(3)对物块，匀速位移为
木板停止运动后减速位移为
由于
，故物块速度减至0也未到达底端
由于
，所以此后物块静止
故整个运动过程中物块的总位移为
练习册系列答案
相关题目
