[题目]如图所示.一横截面为环形的均匀玻璃管.内圆半径为R.外圆半径为2R.圆心为O.PQ为过圆心的水平直线.细光束a平行于PQ射到玻璃管上.入射方向恰好与内圆相切.已知光在真空中的速度为c=3×108m/s.(i)试证明无论该玻璃的折射率多大.光束a经过一次折射后在内圆边界处发生全反射,(ii)若玻璃环的折射率为n=.光束a经过-次折射和一次全反题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，一横截面为环形的均匀玻璃管，内圆半径为R，外圆半径为2R，圆心为O，PQ为过圆心的水平直线。细光束a平行于PQ射到玻璃管上，入射方向恰好与内圆相切。已知光在真空中的速度为c=3×108m/s。

(i)试证明无论该玻璃的折射率多大，光束a经过一次折射后在内圆边界处发生全反射；

(ii)若玻璃环的折射率为n=，光束a经过-次折射和一次全反射，从玻璃管的外圆边界射出(不考虑多次反射情况)，则光线a在玻璃中传播的时间t为多少?(=2.646，计算结果保留两位有效数字)

【答案】(i)见解析；(ii)t=1.1R×10-8s

【解析】

(i)如图

在A点入射由折射定律可得

由几何关系可得

在ABO中由正弦定理得

由全反射临界角规律可得

由以上各式可得

(ii)B点全反射后光线为BE，如图

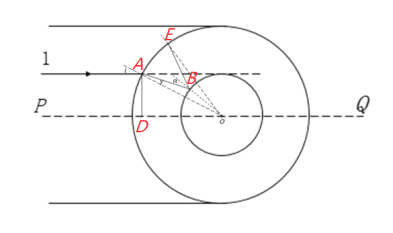
由对称性可知

AB=BE=x

在ABO中由余弦定理可得

由折射率

则时间为

联立得t=1.1R×10-8s

练习册系列答案

相关题目

【题目】如图所示，有四列简谐波同时沿x轴正方向传播，波速分别是v、、、，a、b是x轴上所给定的两点，且.在t时刻a、b两点间四列波的波形分别如图所示，则由该时刻起a点出现波峰的先后顺序依次是图_________；频率由高到低的先后顺序依次是图__________.

A. B. C. D.

【题目】将两点电荷分别固定在x轴上的A、B两点，其坐标分别为(-4，0)和(2，0)，B处点电荷带电量绝对值为Q，两点电荷连线上各点电势随x变化的关系如图所示，其中x=0处电势最高，x轴上M、N两点的坐标分别为(-1，0)和(1，0)，静电力常量为k，则下列说法正确的是(　　)

A.两点电荷一定为异种电荷

B.M点的电场强度大于N点的电场强度

C.M点电场强度大小为

D.正的试探电荷由M点运动到N点的过程，电势能先增大后减小

【题目】斜劈A放在水平地面上，质量为的物体B在外力的共同作用下，沿斜劈表面向下运动。水平向右，沿斜劈表面向下，斜劈A静止受到地面的摩擦力方向向左。若撤去某个力，在B仍向下运动，斜劈A仍静止的情况下，则下列说法中正确的是（　　）

A.若只撤去，B仍向下运动，则A受地面摩擦力方向不变

B.若只撤去，B仍向下运动，则A受地面摩擦力方向可能向右

C.若只撤去，B仍向下运动，则A受地面摩擦力方向不变

D.若只撤去，B仍向下运动，则A所受地面摩擦力方向可能向右

【题目】如图所示，倾角为的斜面上静置一质量为的薄木板，木板的长度为，质量的物块（可视为质点）以初速度沿木板顶端运动，物块与木板之间的动摩擦因数，木板与斜面之间的动摩擦因数，斜面的底端固定一垂直于斜面的挡板，木板的下端距离挡板为，木板与挡板碰撞后立即粘在一起停止运动。设物块与木板之间、木板与斜面之间的动摩擦力等于最大静摩擦力，则（重力加速度)

(1)物块落到斜面上后，木板经过多长时间与挡板相碰；

(2)木板与挡板碰前的速度；

(3)物块总共发生的位移。

【题目】现有三束单束光，其波长关系为.当用光束照射某种金属板时能发生光电效应，飞出的光电子最大动能为，若改用光束照射该金属板，飞出的光电子最大动能为，当改用光束照射该金属板时（）

A.能发生光电效应，飞出的光电子最大动能为

B.能发生光电效应，飞出的光电子最大动能为

C.能发生光电效应，飞出的光电子最大动能为

D.由于光束光子能量最小，该金属板不会发生光电效应

【题目】以的速度竖直向上抛出一物体，忽略空气阻力影响，则物体上升的最大高度________；物体的重力势能为动能的一半时，物体离抛出点的高度_______；物体的重力势能和动能相等时，物体离抛出点的高度________；物体的动能是势能的一半时，物体离抛出点的高度_________；物体的速度减为时，物体离抛出点的高度_________．