题目内容
11.一个质量为0.3kg的弹性小球,在光滑的水平面上以6m/s的速度垂直撞到墙上,碰撞后小球沿相反的方向运动,反弹后的速度大小为4m/s,则碰撞前后小球动量变化量的大小I和碰撞过程中墙对小球做功的大小W为( )| A. | I=3 kg•m/s W=-3J | B. | I=0.6 kg•m/s W=-3J | ||
| C. | I=3 kg•m/s W=7.8J | D. | I=0.6 kg•m/s W=3J |
分析 由于动量是矢量,对于动量的变化量我们应该采用平行四边形法则.
对于同一直线上的动量变化量的求解,我们可以运用表达式△P=P2-P1,但必须规定正方向.
运用动能定理求出碰撞过程中墙对小球做功.
解答 解:规定初速度方向为正方向,初速度v1=6m/s,碰撞后速度v2=-4m/s;△v=v2-v1=-10m/s,负号表示速度变化量的方向与初速度方向相反;
动量变化量为:△P=m•△v=0.3kg×(-10m/s)=-3kg•m/s,所以碰撞前后小球动量变化量的大小为3kg•m/s;
对碰撞过程,对小球由动能定理得:W=△Ek=$\frac{1}{2}m{v}_{2}^{2}-\frac{1}{2}m{v}_{1}^{2}=\frac{1}{2}×0.3×({4}^{2}-{6}^{2})J$=-3J;
故选:A.
点评 对于矢量的加减,我们要考虑方向,动能定理是一个标量等式,对于动能定理的研究,则无需考虑方向.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
16.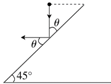 如图所示,一长为$\sqrt{2}$L的木板,倾斜放置,倾角为45°,今有一弹性小球,自与木板上端等高的某处自由释放,小球落到木板上反弹时,速度大小不变,碰撞前后,速度方向与木板夹角相等,欲使小球一次碰撞后恰好落到木板下端,则小球从释放到落到木板底端的过程中,小球的水平位移为( )
如图所示,一长为$\sqrt{2}$L的木板,倾斜放置,倾角为45°,今有一弹性小球,自与木板上端等高的某处自由释放,小球落到木板上反弹时,速度大小不变,碰撞前后,速度方向与木板夹角相等,欲使小球一次碰撞后恰好落到木板下端,则小球从释放到落到木板底端的过程中,小球的水平位移为( )
 如图所示,一长为$\sqrt{2}$L的木板,倾斜放置,倾角为45°,今有一弹性小球,自与木板上端等高的某处自由释放,小球落到木板上反弹时,速度大小不变,碰撞前后,速度方向与木板夹角相等,欲使小球一次碰撞后恰好落到木板下端,则小球从释放到落到木板底端的过程中,小球的水平位移为( )
如图所示,一长为$\sqrt{2}$L的木板,倾斜放置,倾角为45°,今有一弹性小球,自与木板上端等高的某处自由释放,小球落到木板上反弹时,速度大小不变,碰撞前后,速度方向与木板夹角相等,欲使小球一次碰撞后恰好落到木板下端,则小球从释放到落到木板底端的过程中,小球的水平位移为( )| A. | $\frac{L}{2}$ | B. | $\frac{2L}{5}$ | C. | $\frac{4L}{5}$ | D. | $\frac{L}{5}$ |
3.下列哪些做法能使线圈中产生感应电流?( )
| A. | 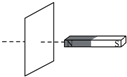 磁铁靠近或远离线圈 | |
| B. | 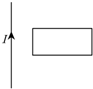 线圈远离或靠近通电导线 | |
| C. | 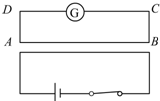 下边电路中通有恒定电流 | |
| D. | 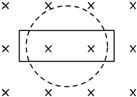 匀强磁场中,周长一定的闭合线圈由矩形变为圆形 |
20.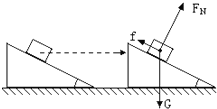 如图所示,三角形滑块从左向右做匀速直线运动,滑块上的物体M与滑块保持相对静止,M受到重力G、摩擦力f和支持力FN的作用.以地面为参考系,此过程中力对M做功的情况,下列说法正确的是( )
如图所示,三角形滑块从左向右做匀速直线运动,滑块上的物体M与滑块保持相对静止,M受到重力G、摩擦力f和支持力FN的作用.以地面为参考系,此过程中力对M做功的情况,下列说法正确的是( )
 如图所示,三角形滑块从左向右做匀速直线运动,滑块上的物体M与滑块保持相对静止,M受到重力G、摩擦力f和支持力FN的作用.以地面为参考系,此过程中力对M做功的情况,下列说法正确的是( )
如图所示,三角形滑块从左向右做匀速直线运动,滑块上的物体M与滑块保持相对静止,M受到重力G、摩擦力f和支持力FN的作用.以地面为参考系,此过程中力对M做功的情况,下列说法正确的是( )| A. | G不做功 | B. | f做正功 | C. | FN不做功 | D. | FN做正功 |
1.人造地球卫星不断加速,其绕地球运行的轨道半径变大,则( )
| A. | 角速度变大 | B. | 线速度变小 | C. | 周期变大 | D. | 向心加速度变小 |
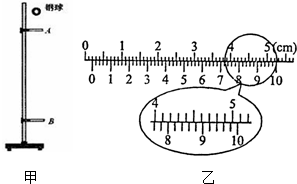 某活动小组利用图甲装置验证机械能守恒定律.钢球自由下落过程中,先、后通过光电门A、B,计时装置测出钢球通过光电门A、B的时间分别为tA、tB钢球通过光电门的平均速率表示钢球心通过光电门的瞬时速度.测出两光电门间的距离为h,当地的重力加速度为g.
某活动小组利用图甲装置验证机械能守恒定律.钢球自由下落过程中,先、后通过光电门A、B,计时装置测出钢球通过光电门A、B的时间分别为tA、tB钢球通过光电门的平均速率表示钢球心通过光电门的瞬时速度.测出两光电门间的距离为h,当地的重力加速度为g.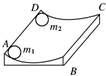 如图所示,一个光滑的圆弧形槽半径为R,圆弧所对的圆心角小于5°.AD的长为s,今有一小球m1以沿AD方向的初速度v从A点开始运动,要使小球m1可以与固定在D点的小球m2相碰撞,那么小球m1的速度v应满足什么条件?
如图所示,一个光滑的圆弧形槽半径为R,圆弧所对的圆心角小于5°.AD的长为s,今有一小球m1以沿AD方向的初速度v从A点开始运动,要使小球m1可以与固定在D点的小球m2相碰撞,那么小球m1的速度v应满足什么条件?