题目内容
6.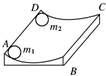 如图所示,一个光滑的圆弧形槽半径为R,圆弧所对的圆心角小于5°.AD的长为s,今有一小球m1以沿AD方向的初速度v从A点开始运动,要使小球m1可以与固定在D点的小球m2相碰撞,那么小球m1的速度v应满足什么条件?
如图所示,一个光滑的圆弧形槽半径为R,圆弧所对的圆心角小于5°.AD的长为s,今有一小球m1以沿AD方向的初速度v从A点开始运动,要使小球m1可以与固定在D点的小球m2相碰撞,那么小球m1的速度v应满足什么条件?
分析 小球m1在AB方向做简谐运动,在AD方向做匀速直线运动,只有当小球经过整数个周期到达D点时,两物体相遇,并根据简谐运动周期,即可求解.
解答 解:把m1的运动分成两个分运动,其一是沿AD方向的匀速运动,其二是沿AB圆弧的运动,实际相当于摆长等于圆弧槽半径的单摆运动,
所以周期:T=2π$\sqrt{\frac{R}{g}}$
小球m1沿AD方向的分运动为匀速直线运动:s=vt
t=nT=2πn$\sqrt{\frac{R}{g}}$(n=1,2,3…)
解得:v=$\frac{s}{2πn}\sqrt{\frac{g}{R}}$(n=1,2,3…)
答:小球m1的速度v应满足$\frac{s}{2πn}\sqrt{\frac{g}{R}}$(n=1,2,3…)时,才能使其恰好碰到小球m2.
点评 此题把匀速直线运动与简谐运动相结合,难点在于不易想到运用简谐运动的周期表达式.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
16.下列说法正确的是( )
| A. | 超声波的频率比普通声波的频率大,更容易发生衍射现象 | |
| B. | 市场上加工烤鸭的远红外烤箱,其加热作用主要是靠紫外线来实现的 | |
| C. | 光从一种介质进入另一种介质时,折射角的大小只取决于两种介质的性质 | |
| D. | 根据狭义相对论,一条沿自身长度方向运动的杆,其长度总比静止时要小一些 |
1.设土星绕太阳的运动是匀速圆周运动,若测得土星到太阳的距离是r,土星绕太阳运动的周期是T,万有引力常量G已知,根据这些数据无法求出的量是( )
| A. | 土星的线速度大小 | B. | 土星的向心力大小 | ||
| C. | 土星的质量 | D. | 太阳的质量 |
11.一个质量为0.3kg的弹性小球,在光滑的水平面上以6m/s的速度垂直撞到墙上,碰撞后小球沿相反的方向运动,反弹后的速度大小为4m/s,则碰撞前后小球动量变化量的大小I和碰撞过程中墙对小球做功的大小W为( )
| A. | I=3 kg•m/s W=-3J | B. | I=0.6 kg•m/s W=-3J | ||
| C. | I=3 kg•m/s W=7.8J | D. | I=0.6 kg•m/s W=3J |
15.下列说法中正确是( )
| A. | 汤姆生发现了电子,并首先提出原子的核式结构模型 | |
| B. | 玻尔理论指出氢原子能级是分立的,所以原子发射光子的频率也是不连续的 | |
| C. | 贝克勒耳发现天然放射现象说明原子核是由质子和中子组成的 | |
| D. | 黑体辐射的强度与温度高低无关 |
16.在经典力学的建立过程中,牛顿和伽利略均作出了重要贡献.下列说法正确的是( )
| A. | 伽利略总结出了惯性定律 | |
| B. | 牛顿提出了牛顿三大定律 | |
| C. | 伽利略总结得出作用力和反作用力之间的关系 | |
| D. | 牛顿利用理想实验推断出匀速运动需要力来维持 |
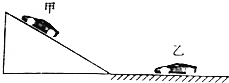 如图所示,某段公路由一段平直的公路与一段斜坡组成,甲车临时停在坡上,司机下车后由于忘记拉“手刹”,甲车开始“溜车”.此时乙车沿平直公路向斜坡驶来,当乙车司机发现正在溜车的甲车时,立即开始刹车,经过2s后刚好停在坡底,并立即开始倒车,以0.6m/s2的加速度做匀加速直线运动,已知乙车司机发现甲车时,甲车距离坡底84m,速度为4m/s,正以0.5m/s2的加速度匀加速滑下,且当甲车到达坡底后,以0.2m/s2的加速度做匀减速运动,若甲、乙两车均视为质点,且甲车通过坡底时无机械能损失,通过计算判断乙车司机能否避免发生撞车?
如图所示,某段公路由一段平直的公路与一段斜坡组成,甲车临时停在坡上,司机下车后由于忘记拉“手刹”,甲车开始“溜车”.此时乙车沿平直公路向斜坡驶来,当乙车司机发现正在溜车的甲车时,立即开始刹车,经过2s后刚好停在坡底,并立即开始倒车,以0.6m/s2的加速度做匀加速直线运动,已知乙车司机发现甲车时,甲车距离坡底84m,速度为4m/s,正以0.5m/s2的加速度匀加速滑下,且当甲车到达坡底后,以0.2m/s2的加速度做匀减速运动,若甲、乙两车均视为质点,且甲车通过坡底时无机械能损失,通过计算判断乙车司机能否避免发生撞车?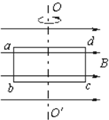 如图所示,匀强磁场的磁感应强度B=2T,匝数n=6的矩形线圈abcd绕中心轴OO′匀速转动,角速度ω=200rad/s.已知ab=0.1m,bc=0.2m,线圈的总电阻R=40Ω,试求:
如图所示,匀强磁场的磁感应强度B=2T,匝数n=6的矩形线圈abcd绕中心轴OO′匀速转动,角速度ω=200rad/s.已知ab=0.1m,bc=0.2m,线圈的总电阻R=40Ω,试求: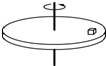 如图所示,置于圆形水平转台上的小物块随转台转动.若转台以角速度ω0=2rad/s.转动时,物块恰好与平台发生相对滑动.现测得小物块与转轴间的距离l1=0.50m,设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2.
如图所示,置于圆形水平转台上的小物块随转台转动.若转台以角速度ω0=2rad/s.转动时,物块恰好与平台发生相对滑动.现测得小物块与转轴间的距离l1=0.50m,设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2.