题目内容
19.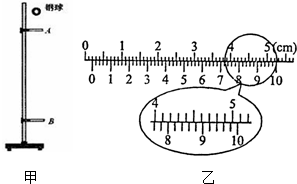 某活动小组利用图甲装置验证机械能守恒定律.钢球自由下落过程中,先、后通过光电门A、B,计时装置测出钢球通过光电门A、B的时间分别为tA、tB钢球通过光电门的平均速率表示钢球心通过光电门的瞬时速度.测出两光电门间的距离为h,当地的重力加速度为g.
某活动小组利用图甲装置验证机械能守恒定律.钢球自由下落过程中,先、后通过光电门A、B,计时装置测出钢球通过光电门A、B的时间分别为tA、tB钢球通过光电门的平均速率表示钢球心通过光电门的瞬时速度.测出两光电门间的距离为h,当地的重力加速度为g.①用游标卡尺测量钢球的直径,读数如图乙所示,钢球直径为D=0.194cm.
②要验证机械能守恒,只要比较D.
A.D2($\frac{1}{{{t}_{A}}^{2}}$-$\frac{1}{{t}_{B}2}$)与gh是否相等
B.D2($\frac{1}{{{t}_{A}}^{2}}$-$\frac{1}{{t}_{B}2}$)与2gh是否相等
C.D2($\frac{1}{{{t}_{A}}^{2}-{{t}_{B}}^{2}}$)与gh
D.D2($\frac{1}{{{t}_{B}}^{2}}$-$\frac{1}{{{t}_{A}}^{2}}$)与2gh
球通过光电门的平均速度<(选填“>”或“<”)钢球球心通过光电门的瞬时速度.
分析 (1)解决本题的关键掌握游标卡尺读数的方法,主尺读数加上游标读数,不需估读.
(2)利用小球通过光电门的平均速度来代替瞬时速度,由此可以求出小铁球通过光电门时的瞬时速度,根据机械能守恒的表达式可以求出所要求的关系式.
(3)根据匀变速直线运动的规律判断求解.
解答 解:(1)游标卡尺的主尺读数为:0.1cm,游标尺上第10个刻度和主尺上某一刻度对齐,所以游标读数为0.02×47mm=0.94mm,所以最终读数为:0.194cm.
(2)利用小球通过光电门的平均速度来代替瞬时速度,故:v=$\frac{D}{t}$,
根据机械能守恒的表达式有:mgh=$\frac{1}{2}$m${D}^{2}(\frac{1}{{t}_{B}^{2}}-\frac{1}{{t}_{A}^{2}})$
即只要比较${D^2}(\frac{1}{t_B^2}-\frac{1}{t_A^2})$与2gh是否相等,
故选:D.
(3)根据匀变速直线运动的规律得钢球通过光电门的平均速度等于这个过程中中间时刻速度,
所以钢球通过光电门的平均速度<钢球球心通过光电门的瞬时速度.
故答案为:(1)0.194;(2)D;(3)<
点评 对于基本测量仪器如游标卡尺、螺旋测微器等要了解其原理,正确使用这些基本仪器进行有关测量.
无论采用什么样的方法来验证机械能守恒,明确其实验原理都是解决问题的关键,同时在处理数据时,要灵活应用所学运动学的基本规律.

练习册系列答案
相关题目
9.一根长0.5m的绳子,当它受到5.8N的拉力时,即可被拉断,绳的一端拴一个质量为0.4kg的小球,使小球在竖直平面内绕绳的另一端做圆周运动,当小球通过最低点时绳子恰好被拉断,则绳即将断开时小球受到的向心力大小是(取g=10m/s2)( )
| A. | 8 N | B. | 5.8N | C. | 5.4 N | D. | 1.8 N |
11.一个质量为0.3kg的弹性小球,在光滑的水平面上以6m/s的速度垂直撞到墙上,碰撞后小球沿相反的方向运动,反弹后的速度大小为4m/s,则碰撞前后小球动量变化量的大小I和碰撞过程中墙对小球做功的大小W为( )
| A. | I=3 kg•m/s W=-3J | B. | I=0.6 kg•m/s W=-3J | ||
| C. | I=3 kg•m/s W=7.8J | D. | I=0.6 kg•m/s W=3J |
8.质量为3m的小车,运动速度为v0,与质量为2m的静止小车碰撞后连在一起运动,则碰撞后两车的总动量为( )
| A. | $\frac{3}{5}$mv0 | B. | 2mv0 | C. | 3mv0 | D. | 5mv0 |
9.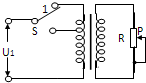 如图所示为一理想变压器,S为一单刀双掷开关,P为滑动变阻器的滑动片,U1为加在原线圈两端的电压,I1为原线圈中的电流那么( )
如图所示为一理想变压器,S为一单刀双掷开关,P为滑动变阻器的滑动片,U1为加在原线圈两端的电压,I1为原线圈中的电流那么( )
 如图所示为一理想变压器,S为一单刀双掷开关,P为滑动变阻器的滑动片,U1为加在原线圈两端的电压,I1为原线圈中的电流那么( )
如图所示为一理想变压器,S为一单刀双掷开关,P为滑动变阻器的滑动片,U1为加在原线圈两端的电压,I1为原线圈中的电流那么( )| A. | 保持U1及P的位置不变,S由1拨到2时,I1将增大 | |
| B. | 保持U1及P的位置不变,S由2拨到1时,R消耗的功率增大 | |
| C. | 保持U1不变,S拨到1,当P下滑时,I1将增大 | |
| D. | 保持P的位置不变时,S拨到1,当U1增大时,I1将增大 |
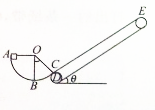 如图所示为一传送带,竖直光滑圆弧轨道ABC半径R=1m,O为圆心,圆心角为127°,传送带DE与水平方向的夹角为θ=30°,长为L=4m.圆弧轨道的末端C点有一段小圆弧与传送带D点相切,现从与O点等高处的A点无初速度释放一物体,经圆弧轨道由C点滑上传送带,假设物体由圆弧轨道滑上传送带的速度不变,物体与传送带间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,g取10m/s2.
如图所示为一传送带,竖直光滑圆弧轨道ABC半径R=1m,O为圆心,圆心角为127°,传送带DE与水平方向的夹角为θ=30°,长为L=4m.圆弧轨道的末端C点有一段小圆弧与传送带D点相切,现从与O点等高处的A点无初速度释放一物体,经圆弧轨道由C点滑上传送带,假设物体由圆弧轨道滑上传送带的速度不变,物体与传送带间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,g取10m/s2.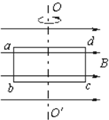 如图所示,匀强磁场的磁感应强度B=2T,匝数n=6的矩形线圈abcd绕中心轴OO′匀速转动,角速度ω=200rad/s.已知ab=0.1m,bc=0.2m,线圈的总电阻R=40Ω,试求:
如图所示,匀强磁场的磁感应强度B=2T,匝数n=6的矩形线圈abcd绕中心轴OO′匀速转动,角速度ω=200rad/s.已知ab=0.1m,bc=0.2m,线圈的总电阻R=40Ω,试求: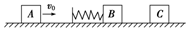 如图.光滑水平直轨道上有三个质量均为m的物块A、B、C,B的左侧固定一轻弹簧(弹簧左侧的挡板质量不计).A以速度v0向B运动,压缩弹簧,当A、B速度相等时,B与C恰好相碰并粘接在一起,然后继续运动.假设B和C碰撞过程时间极短,求从A开始压缩弹簧直至与弹簧分离的过程中:
如图.光滑水平直轨道上有三个质量均为m的物块A、B、C,B的左侧固定一轻弹簧(弹簧左侧的挡板质量不计).A以速度v0向B运动,压缩弹簧,当A、B速度相等时,B与C恰好相碰并粘接在一起,然后继续运动.假设B和C碰撞过程时间极短,求从A开始压缩弹簧直至与弹簧分离的过程中: