题目内容
两颗靠得很近的天体称为双星，它们以两者连线上某点O为圆心作角速度相同的匀速圆周运动，这样就不至于由于万有引力而吸引在一起，设两双星质量分别为m和M，M=3m．两星球间的距离为L，如图，在这两个星球间的相互万有引力作用下，绕它们连线上某点O转动，求：
（1）OM间的距离r1为多少？
（2）他们的运动周期为多少？（引力常数G为已知）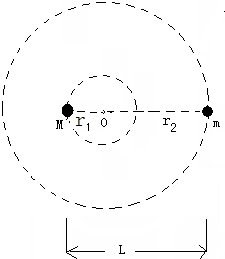
（1）OM间的距离r1为多少？
（2）他们的运动周期为多少？（引力常数G为已知）
（1）双星向心力F和角速度ω大小相等，根据万有引力提供向心力：
对M有：G
=Mω2r1 ①
对m有：G
=mω2r2
解得：
=
=
又 r1+r2=L
所以 r1=
L
（2）由①式得：
ω2=
又因为ω=
所以ω2=
=
解得：T=πL
答：（1）、OM间的距离r1为
L；
（2）、他们的运动周期为πL
．
对M有：G
| Mm |
| L2 |
对m有：G
| Mm |
| L2 |
解得：
| r1 |
| r2 |
| m |
| M |
| 1 |
| 3 |
又 r1+r2=L
所以 r1=
| 1 |
| 4 |
（2）由①式得：
ω2=
| Gm |
| L2r1 |
又因为ω=
| 2π |
| T |
所以ω2=
| 4π2 |
| T2 |
| Gm |
| L2r1 |
解得：T=πL
|
答：（1）、OM间的距离r1为
| 1 |
| 4 |
（2）、他们的运动周期为πL
|
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
