题目内容
如图所示，一个重为G的小球套在竖直放置的半径为R的光滑圆环上，一个劲度系数为k，自然长度为L（L＜2R）的轻质弹簧，一端与小球相连，另一端固定在大环的最高点，求小球处于静止状态时，弹簧与竖直方向的夹角φ．
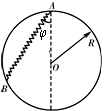
φ = arcos?
解析:
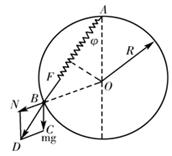
小球受力如图所示，有竖直向下的重力G，弹簧的弹力F， 圆环的弹力N，N沿半径方向背离圆心O．
利用合成法，将重力G和弹力N合成，合力F合应与弹簧弹力F平衡观察发现，图中力的三角形△BCD与△AOB相似，设AB长度为l由三角形相似有：
= 
= ，即得F =
另外由胡克定律有F = k（l-L），而l = 2Rcosφ?
联立上述各式可得：cosφ = ，φ = arcos?
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
如图所示，一个重为G=20N的木块放在倾角30°的光滑斜面上，被一根劲度系数k=250N/m的轻弹簧拉着．该弹簧原长l0=0.20m，求：
如图所示，一个重为G的均匀球体放在倾角θ=37°的光滑斜面上，并被斜面上一个竖直的光滑挡板挡住处于平衡状态．请解答下列两个问题：
如图所示，一个重为G的小球套在竖直放置的半径为R的光滑圆环上，一个劲度系数为k，自然长度为L（L＜2R）的轻质弹簧，一端与小球相连，另一端固定在大环的最高点，求小球处于静止状态时，弹簧与竖直方向的夹角φ．
如图所示，一个重为G的小环套在竖直放置的半径为R的光滑大圆环上，一个劲度系数为k，原长为L（L＜2R）的轻弹簧，一端固定在大圆环顶点A，另一端与小环相连，小环在大圆环上可无摩擦滑动．环静止于B点时，则弹簧与竖直方向的夹角θ为多少？（提示：用相似三角形法求解）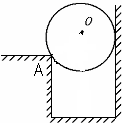
如图所示，一个重为G、半径为R的质量分布不均匀小球被夹在竖直的墙壁和A点之间，已知重心O（在球心正上方）与A点的连线长为