题目内容
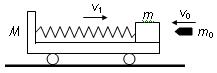
（11分）如图（1）所示，在光滑的水平面上有甲、乙两辆小车，质量为30kg的小孩乘甲车以5m/s的速度水平向右匀速运动，甲车的质量为15kg，乙车静止于甲车滑行的前方，两车碰撞前后的位移随时间变化图象如图（2）所示。
求：（1）甲乙两车碰撞后的速度大小；
（2）乙车的质量；
（3）为了避免甲乙两车相撞，小孩至少以多大的水平速度从甲车跳到乙车上？
求：（1）甲乙两车碰撞后的速度大小；
（2）乙车的质量；
（3）为了避免甲乙两车相撞，小孩至少以多大的水平速度从甲车跳到乙车上？
（1）甲车的速度大小为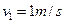
，乙车的速度大小为v2=3m/s
（2）
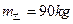
（3）
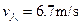
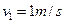，乙车的速度大小为v2=3m/s（2）
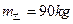
（3）
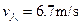
（1）由图可知，碰撞后甲车的速度大小为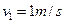 （1分）
乙车的速度大小为v2="3m/s " （1分）
（2）在碰撞过程中，三者组成的系统满足动量守恒。
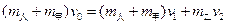
（2分）
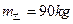解得： （1分）
（3）设人跳向乙车的速度为v人,由动量守恒定律得
人跳离甲车：
（1分）
人跳至乙车：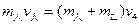
（1分）
为使二车避免相撞，应满足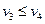
（2分）
取“=”时，人跳离甲车的速度最小，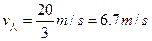
（2分）
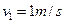（1分）乙车的速度大小为v2="3m/s " （1分）
（2）在碰撞过程中，三者组成的系统满足动量守恒。
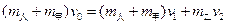
（2分）解得：
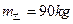（1分）（3）设人跳向乙车的速度为v人,由动量守恒定律得
人跳离甲车：
（1分）人跳至乙车：
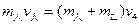（1分）为使二车避免相撞，应满足
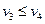（2分）取“=”时，人跳离甲车的速度最小，
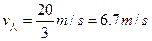（2分）
练习册系列答案
阅读快车系列答案
相关题目
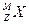连续经过三次α衰变和两次β衰变．若最后变成另一种元素的原子核Y，则新核Y的正确写法是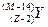
、
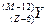
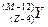
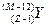
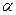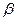和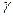
三种射线，由铅盒的小孔射出，在小孔外放一张铝箔，铝箔后的空间有一匀强电场。射线进入电场后，变为a、b两束，射线a沿原来方向行进，射线b发生了偏转，如图所示，则图中的射线a为_________射线，射线b为___________射线。
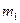的光滑弧形槽静止在光滑水平面上，底部与水平面平滑连接。一个质量为
的小球从槽
高处由静止开始下滑，要使小球能与弧形槽发生第二次作用，
