题目内容
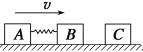
【题目】如图所示,有两个高低不同的水平面,高水平面光滑,低水平面粗糙.一质量为5kg、长度为2m的长木板靠在高水平面边缘A点,其表面恰好与高水平面平齐,长木板与低水平间的动摩擦因数为0.05,一质量为1kg可视为质点的滑块静止放置,距A点距离为3m,现用大小为6N、水平向右的外力拉小滑块,当小滑块运动到A点时撤去外力,滑块以此时的速度滑上长木板.滑块与平板车间的动摩擦因数为0.5,取g=10m/s2 . 求: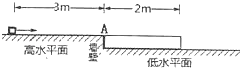
(1)滑块滑动到A点时的速度大小;
(2)滑块滑动到长木板上时,滑块和长木板的加速度大小分别为多少?
(3)通过计算说明滑块能否从平板车的右端滑出.
【答案】
(1)解:根据牛顿第二定律有:F=ma
根据运动学公式有:v2=2aL0
联立方程带入数据解得:v=6m/s
其中m、F分别为滑块的质量和受到的拉力,a是滑块的加速度,v即是滑块滑到A点时的速度大小,L0是滑块在高水平面上运动位移
答:滑块滑动到A点时的速度大小6m/s;
(2)根据牛顿第二定律有:
对滑块有:μ1mg=ma1
带入数据解得:a1=5m/s2
对长木板有:μ1mg﹣μ2(m+M)g=Ma2,
带入数据解得:a2=0.4m/s2.
其中M为长木板的质量,a1、a2分别是此过程中滑块和长木板的加速度,μ1、μ2分别是滑块与长木板间和长木板与低水平面间的动摩擦因数
答:滑块滑动到长木板上时,滑块和长木板的加速度大小分别为5m/s2,0.4m/s2
(3)设小滑块不滑出长木板,从小滑块滑上长木板到两者相对静止所用时间为t
则:v﹣a1t=a2t
带入数据解得:t= ![]() s,
s,
则此过程中小滑块的位移为: ![]()
长木板的位移为: ![]()
![]()
式中L=2m为长木板的长度,所以小滑块滑出长木板右端
答:滑块能从平板车的右端滑出
【解析】(1)因为高水平面光滑,滑块仅受到水平向右的外力作用,此外立即为合外力,根据牛顿第二定律可以求出滑块的加速度。再根据匀变速直线运动速度和位移加速度的公式,可以求出滑块滑动到A点时的速度大小。
(2)以滑块和长木板为研究对象,分别进行受力分析,滑块所受的合外力为滑动摩擦力,长木板所受合外力为滑块和地面的摩擦力之和,根据牛顿第二定律可以分别求出加速度。
(3)根据临界的方法求解,先假设从小滑块滑上长木板到两者相对静止所用时间,根据匀变速直线运动速度时间公式可以列式求出,再根据匀变速直线运动公式求出相对静止时的位移。最后与长木板的长度比较即可。
【考点精析】利用匀变速直线运动的速度、位移、时间的关系对题目进行判断即可得到答案,需要熟知速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案【题目】如图所示,一倾角为37°的斜面固定在水平地面上,质量m=1kg的物体在平行于斜面向上的恒力F作用下,从A点由静止开始运动,到达B点时立即撤去拉力F.此后,物体到达C点时速度为零.每隔0.2s通过速度传感器测得物体的瞬时速度,下表给出了部分测量数据.(取 sin37°=0.6.cos37°=0.8)试求:
t/s | 0.0 | 0.2 | 0.4 | … | 2.2 | 2.4 | … |
v/ms﹣1 | 0.0 | 1.0 | 2.0 | … | 3.3 | 1.2 | … |
(1)斜面的摩擦系数μ;
(2)恒力F的大小;
(3)t=1.6s时物体的瞬时速度.