题目内容
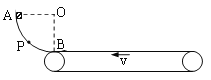
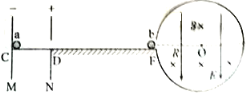
【题目】如图,M、N是电压U=10V的平行板电容器两极板,与绝缘水平轨道CF相接,其中CD段光滑,DF段粗糙、长度x=1.0m。F点紧邻半径为R的绝缘圆简(图示为圆筒的横截面),圆筒上开一小孔与圆心O在同一水平面上,圆筒内存在磁感应强度B=0.5T、方向垂直纸面向里的匀强磁场和方向竖直向下的匀强电场E。一质量m=0.01kg、电荷量q=-0.02C的小球a从C点静止释放,运动到F点时与质量为2m、不带电的静止小球b发生碰撞,碰撞后a球恰好返回D点,b球进入圆筒后在竖直面内做圆周运动。不计空气阻力,小球a、b均视为质点,碰时两球电量平分,小球a在DF段与轨道的动摩因数μ=0.2,重力加速度大小g=10m/s2。求
(1)圆筒内电场强度的大小;
(2)两球碰撞时损失的能量;
(3)若b球进入圆筒后,与筒壁发生弹性碰撞,并从N点射出,则圆筒的半径。
【答案】(1)20N/C;(2)0J;(3) ![]() n≥3的整数)
n≥3的整数)
【解析】
(1)小球b要在圆筒内做圆周运动,应满足:![]() Eq=2mg
Eq=2mg
解得:E=20 N/C
(2)小球a到达F点的速度为v1,根据动能定理得:Uq-μmgx=![]() mv12
mv12
小球a从F点的返回的速度为v2,根据功能关系得:μmgx=![]() mv22
mv22
两球碰撞后,b球的速度为v,根据动量守恒定律得:mv1=-mv2+2mv
则两球碰撞损失的能量为:ΔE=![]() mv12-
mv12-![]() mv22-
mv22-![]() mv2
mv2
联立解得:ΔE=0
(3)小球b进入圆筒后,与筒壁发生n-1次碰撞后从N点射出,轨迹图如图所示:
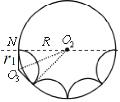
每段圆弧对应圆筒的圆心角为![]() ,则在磁场中做圆周运动的轨迹半径:r1=
,则在磁场中做圆周运动的轨迹半径:r1=![]()
粒子在磁场中做圆周运动:![]()
联立解得:![]() (n≥3的整数)
(n≥3的整数)

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目