题目内容
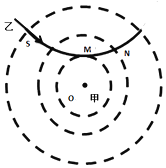
【题目】如图所示,是一个半径为R的半圆柱形透明物体的截面图。现有平行于轴线OA的单色光从左侧射入透明物体,已知从距圆心![]() 的P点射入透明物体的光,经过透明物体后通过轴线OA上的Q点,Q点距圆心O的距离为
的P点射入透明物体的光,经过透明物体后通过轴线OA上的Q点,Q点距圆心O的距离为![]() 。求:
。求:

(1)该透明物体的折射率;
(2)能够从透明物体圆形边界射出的光(不考虑多次反射的情况),其入射光的范围。
【答案】(1) ![]() (2) 入射光的范围在距O点小于
(2) 入射光的范围在距O点小于![]() 的距离内
的距离内
【解析】
(i) 如图,
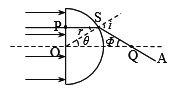
设光在弧面上的入射点为S,入射角为r,折射角为i,OS与OA夹角为![]() ,由几何关系:
,由几何关系:
![]()
设S、Q间的距离分别为![]() ,
,
由题意可得O、Q间距:![]()
在![]() OSQ中,由余弦定理得:
OSQ中,由余弦定理得:![]()
代入数据得:![]()
![]() OSQ为等腰三角形
OSQ为等腰三角形
设SQ与OA的夹角为Φ,
由几何知识可得:Φ =θ,i=Φ +θ
由折射定律:![]()
代入数据得:![]()
(ii)设临界角为C,入射光离O的最远距离为d,由折射定律:![]()
根据几何关系:![]()
代入数据得:![]() ,即入射光的范围在距O点小于
,即入射光的范围在距O点小于![]() 的距离内。
的距离内。

练习册系列答案
相关题目
【题目】自主品牌比亚迪汽车,2018年度新能源汽车总销量超越全球知名品牌特斯拉,旗下热销车型比亚迪唐好评如潮。表格中是纯电动唐的部分技术参数,分析可知( )
续航里程(km,特定工况下) | 520 |
整备质量(kg) | 2155 |
最高车速(km/h) | 160 |
电池组储能(kwh) | 82.8 |
电机额定机械功率(kw) | 180 |
电池组总功率与电机机械功率的转化效率 | 80% |
A. 工况条件下百公里耗电量17.3kwh
B. 电池组容量约为2.98×108C
C. 若持续额定机械功率工作,可工作约0.46h
D. 在水平直道上以最高车速行驶时,受到的阻力约为4050N