��Ŀ����
����Ŀ����ͼ��POQ���۳�60��ǵĹ̶�����ֱƽ���ڵĹ⻬�������죬���������ֱ���߶Գƣ�OP=OQ=L= ![]() m������װ�ô��ڴ�ֱ����ƽ��������㹻�����ǿ�ų��У��Ÿ�Ӧǿ����ʱ��仯����ΪB=1��8t��T����һ����Ϊ1kg����ΪL������Ϊ1������ϸ���ȵĵ����������OP��OQ���е�a��bλ�ã����Ÿ�Ӧǿ�ȱ�ΪB1=0.5T �ֲ��䣬ͬʱ��������������������������˶����뿪����ʱ���ٶ�Ϊv=3.6m/s��������뵼��ʼ�ձ������ýӴ���������費�ƣ��������ٶ�Ϊg=10m/s2 �� �������
m������װ�ô��ڴ�ֱ����ƽ��������㹻�����ǿ�ų��У��Ÿ�Ӧǿ����ʱ��仯����ΪB=1��8t��T����һ����Ϊ1kg����ΪL������Ϊ1������ϸ���ȵĵ����������OP��OQ���е�a��bλ�ã����Ÿ�Ӧǿ�ȱ�ΪB1=0.5T �ֲ��䣬ͬʱ��������������������������˶����뿪����ʱ���ٶ�Ϊv=3.6m/s��������뵼��ʼ�ձ������ýӴ���������費�ƣ��������ٶ�Ϊg=10m/s2 �� �������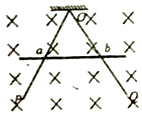
��1���������ǰ��·�е����Ĵ�С������
��2����������ĩ��ʱ�ļ��ٶȴ�С��
��3���˶������в����Ľ����ȣ�
���𰸡�
��1���⣺�������ǰ����Ӧ�綯��Ϊ��
E= ![]() =S
=S ![]() =
= ![]() =
= ![]() V��
V��
��Ӧ����Ϊ��I= ![]() =
= 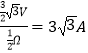 ��
��
����ζ���֪����Ӧ�����ķ���Ϊ˳ʱ�뷽��
�𣺽������ǰ��·�е����Ĵ�СΪ ![]() A��������˳ʱ�룻
A��������˳ʱ�룻
��2����������ĩ��ʱ�ģ���Ӧ�綯��Ϊ��E=BLv=0.5�� ![]() ��3.6=1.8
��3.6=1.8 ![]() V��
V��
��Ӧ����Ϊ��I= ![]() ��
��
��������F=BIL=0.5��1.8 ![]() ��
�� ![]() =2.7N��
=2.7N��
����ţ�ٵڶ����ɣ��У�mg��F=ma��
��ã�a=g�� ![]() =10��
=10�� ![]() =7.3m/s2��
=7.3m/s2��
�𣺻�������ĩ��ʱ�ļ��ٶȴ�СΪ7.3m/s2��
��3���������غ�ã�mgh= ![]() mv2+Q
mv2+Q
h= ![]() L
L
��ã�Q= ![]() ��
�� ![]() mv2=
mv2= ![]() =1.02J��
=1.02J��
���˶������в����Ľ�����Ϊ1.02J��
����������1������Ÿ�Ӧ����,һ��������˼·,һ���Ǹ����������з���,����һ���Ǵ������غ�ĽǶȽ���,���ݷ����ڵ�Ÿ�Ӧ������ʽ����Ӧ�綯�ƴ�С������ŷķ��������Ӧ������С��������ζ��ɺͰ��ඨ���жϸ�Ӧ�����ķ���
��2���������ĽǶȽ��з���,�����иʽ����Ӧ�綯�ƣ�����ŷķ��������Ӧ���������ݰ�������ʽ��ⰲ����������ţ�ٵڶ�������ʽ�����ٶȣ�
��3���������غ�ĽǶȽ��з���,���������غ㶨��,���ٵ���������ת����Ϊ���ܺ�����,��ʽ����˶������в����Ľ����ȣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�