题目内容
一质量为m的物块在倾角为
的足够长斜面上匀减速下滑．现对物块施加一个竖直向下的恒力F，如图所示．则物块减速为零的时间将
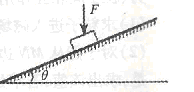
| A．变大 | B．变小 | C．不变 | D．不能确定 |
B
解析试题分析：未施加F时，根据牛顿第二定律，物块的加速度a==gsinθ-μgcosθ．施加F后，根据牛顿第二定律，物块的加速度 (F+mg)sinθ?μ(F+mg)cosθ=ma′，：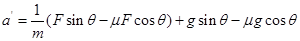
．知a′＞a．加速度增大，初速度不变，则运动时间变小．故B正确．
考点：牛顿定律的应用。
一诺书业暑假作业快乐假期云南美术出版社系列答案如图，质量为MA、MB的A、B两小球分别连在弹簧两端，B端用细线固定在倾角为30°的光滑斜面上，若不计弹簧质量，在线被剪断瞬间，A、B两球的加速度分别为（ ）
A．0和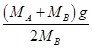
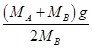B． 和0
C．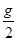 
和0 D．都等于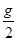
如图甲所示，物体受到水平推力F的作用在粗糙水平面上做直线运动．通过力传感器和速度传感器监测到推力F、物体速度v随时间t变化的规律如图乙所示．取g＝10 m/s2.则( )
| A．物体的质量m＝1.0 kg |
| B．物体与水平面间的动摩擦因数μ＝0.20 |
| C．第2秒内物体克服摩擦力做的功W＝1.8J |
D．前2秒内推力F做功的平均功率 ＝1.5W |
如图所示，固定坡道倾角为θ，顶端距光滑水平面的高度为h，一可视为质点的小物块质量为m，从坡道顶端由静止滑下，经过底端O点进入水平面时无机械能损失，为使小物块制动将轻弹簧的一端固定在水平面左侧M处的竖直墙上，弹簧自由伸长时右侧一端恰好位于O点。已知小物块与坡道间的动摩擦因数为μ，重力加速度为g,则下列说法正确的是
| A．小物块在倾斜轨道上运动时，下滑的加速度比上滑的加速度小 |
| B．当小物块压缩弹簧到最短时，物块的重力势能完全转化为弹簧的弹性势能 |
C．小物块返回倾斜轨道时所能达到的最大高度为 |
| D．小物块在往返运动的整个过程中损失的机械能为mgh |
有一辆质量为170kg、额定功率为1440W的太阳能试验汽车，安装有约6m2的太阳能电池板和蓄能电池，该电池板在有效光（垂直照射在电池板上的太阳光）照射条件下单位面积输出的电功率为30W/ m2。若驾驶员的质量为70kg，汽车最大行驶速度为90km/h。假设汽车行驶时受到的空气阻力与其速度成正比，则汽车（ ）
| A．以最大速度行驶时牵引力大小为57.6N |
| B．以额定功率启动时的加速度大小为0.24 m/s2 |
| C．保持最大速度行驶1 h至少需要有效光照8 h |
| D．直接用太阳能电池板提供的功率可获得3.13 m/s的最大行驶速度 |
A．
B．
C．
D．
如图所示，m=5kg的物体A在平行于斜面向上的外力F作用下，沿斜面以a=5m/s2加速向上运动，已知F="65" N，斜面倾角θ=37o，则突然撤去F的瞬时，A的加速度为（ ）
| A．2m/s2，沿斜面向上 | B．4m/s2，沿斜面向 |
| C．6m/s2，沿斜面向下 | D．8m/s2，沿斜面向下 |