题目内容
如图所示，固定坡道倾角为θ，顶端距光滑水平面的高度为h，一可视为质点的小物块质量为m，从坡道顶端由静止滑下，经过底端O点进入水平面时无机械能损失，为使小物块制动将轻弹簧的一端固定在水平面左侧M处的竖直墙上，弹簧自由伸长时右侧一端恰好位于O点。已知小物块与坡道间的动摩擦因数为μ，重力加速度为g,则下列说法正确的是
| A．小物块在倾斜轨道上运动时，下滑的加速度比上滑的加速度小 |
| B．当小物块压缩弹簧到最短时，物块的重力势能完全转化为弹簧的弹性势能 |
C．小物块返回倾斜轨道时所能达到的最大高度为 |
| D．小物块在往返运动的整个过程中损失的机械能为mgh |
ACD
解析试题分析：小物块在倾斜轨道上运动时，下滑的加速度大小
，上滑的加速度大小
，故A正确；由于在倾斜轨道上运动时要克服摩擦力做功，所以当小物块压缩弹簧到最短时，物块的重力势能转化为弹簧的弹性势能和摩擦热，故B错误；由动能定理得下滑到O点时mgh-μmgcosθ?
=
mv2，又水平道光滑，由机械能守恒定律得mv2＝Ep，设小物块返回倾斜轨道时能够上升的最大高度为h1，由动能定理得-mgh1-μmgcosθ?
=0-mv2，解得：h1＝，故C正确；由能量守恒定律可知小物块在往返运动的整个过程中机械能全部转化为内能，故损失的机械能为mgh，D正确。
考点：牛顿第二定律，动能定理，机械能守恒定律，能量守恒定律
如图所示，一夹子夹住木块，在力F作用下向上提升．夹子和木块的质量分别为m、M，夹子与木块两侧间的最大静摩擦力均为f.若木块不滑动，力F的最大值是
A． | B． |
C． －(m＋M)g | D．＋ (m＋M)g |
为了让乘客乘车更为舒适，某探究小组设计了一种新的交通工具，乘客的座椅能随着坡度的变化而自动调整，使得座椅始终保持水平，当此车加速上坡时，乘客
| A．支持力小于重力 |
| B．支持力大于重力 |
| C．受到水平向左的摩擦力作用 |
| D．所受力的合力沿斜面方向向下 |
据中新社北京2月26日电，中国军队2013年将举行近40场军事演习，以提高信息化条件下威慑和实战能力。若在某次军事演习中，一跳伞队员在t=0时由静止的直升机上跳下，先做自由落体运动，在t1时刻，速度达到v1时打开降落伞，做减速运动，在t2时刻以速度v2着地，他的速度—时间图象如图所示。（跳伞队员的质量为M，降落伞的质量为m）。据此，下列分析正确的是：
| A．在0～t2时间内，降落伞和跳伞队员的机械能逐渐减小 |
| B．降落伞打开后降落伞和跳伞队员所受的阻力与速率成正比 |
| C．若第一个跳伞队员跳下后，经过时间t1，第二个跳伞队员跳下，则他们在空中的距离先增大后减小 |
D．t1～t2时间内阻力对降落伞和跳伞队员所做的功为 |
如图所示，空间存在一有边界的条形匀强磁场区域，磁场方向与竖直平面（纸面）垂直，磁场边界的间距为L。一个质量为m、边长也为L的正方形导线框沿竖直方向运动，线框所在平面始终与磁场方向垂直，且线框上、下边始终与磁场的边界平行。t＝0时刻导线框的上边恰好与磁场的下边界重合（图中位置Ⅰ），导线框的速度为v0。经历一段时间后，当导线框的下边恰好与磁场的上边界重合时（图中位置Ⅱ），导线框的速度刚好为零。此后，导线框下落，经过一段时间回到初始位置Ⅰ。则
| A．上升过程中，导线框的加速度逐渐增大 |
| B．下降过程中，导线框的加速度逐渐增大 |
| C．上升过程中合力做的功与下降过程中的相等 |
| D．上升过程中克服安培力做的功比下降过程中的多 |
一质量为m的物块在倾角为
的足够长斜面上匀减速下滑．现对物块施加一个竖直向下的恒力F，如图所示．则物块减速为零的时间将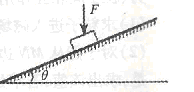
| A．变大 | B．变小 | C．不变 | D．不能确定 |
如下图所示，一个带负电的滑环套在水平且足够长的粗糙的绝缘杆上，整个装置处于方向如图所示的匀强磁场B中．现给滑环施以一个水平向右的瞬时速度，使其由静止开始运动，则滑环在杆上的运动情况可能是( )
| A．始终做匀速运动 |
| B．开始做减速运动，最后静止于杆上 |
| C．先做加速运动，最后做匀速运动 |
| D．先做减速运动，最后做匀速运动 |
站在电梯上的人，当电梯竖直减速下降时，下面说法正确的是
| A．电梯对人的支持力小于人对电梯的压力 |
| B．电梯对人的支持力大等于人对电梯的压力 |
| C．电梯对人的支持力小于人的重力 |
| D．电梯对人的支持力大于人的重力 |
如图，物体将轻质弹簧压缩后由静止释放，物体在弹力的推动下沿粗糙水平面向右运动，不计空气阻力，物体从开始运动到与弹簧分离的全过程中
| A．物体做匀加速运动 |
| B．物体的加速度的大小逐渐减小 |
| C．物体的速度先增大后减小 |
| D．物体与弹簧分离时速度最大 |