题目内容
如图,质量为MA、MB的A、B两小球分别连在弹簧两端,B端用细线固定在倾角为30°的光滑斜面上,若不计弹簧质量,在线被剪断瞬间,A、B两球的加速度分别为( )
A.0和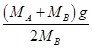 B.
B. 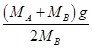 和0
和0
C. 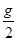 和0 D.都等于
和0 D.都等于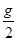
A
解析试题分析:在剪断细线之前,A处于平衡状态,所以弹簧的拉力等于A的重力沿斜面的分力.在剪断细线的瞬间,绳子上的拉力立即减为零,而弹簧的伸长量没有来得及发生改变,故弹力不变,所以A的受力情况没有变化,故A球的加速度为零;在剪断细线之前,对B球进行受力分析,B受到重力、弹簧对它斜向下的拉力、支持力及细线的拉力,在剪断细线的瞬间,细线的拉力立即减为零,对B球进行受力分析,则B受到到重力、弹簧的向下拉力、支持力.因弹簧的拉力大小为 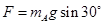 ,所以根据牛顿第二定律得:B的加速度为
,所以根据牛顿第二定律得:B的加速度为 .故BCD错误,A正确.所以选D.
.故BCD错误,A正确.所以选D.
考点:牛顿第二定律;胡克定律及共点力作用下物体的平衡.

如图所示,三个物体质量分别为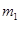 =1.0kg、
=1.0kg、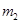 =2.0kg、
=2.0kg、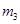 ="3.0kg" ,已知斜面上表面光滑,斜面倾角
="3.0kg" ,已知斜面上表面光滑,斜面倾角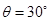 ,
,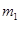 和
和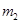 之间的动摩擦因数μ=0.8。不计绳和滑轮的质量和摩擦。初始用外力使整个系统静止,当撤掉外力时,
之间的动摩擦因数μ=0.8。不计绳和滑轮的质量和摩擦。初始用外力使整个系统静止,当撤掉外力时,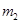 将(g=10m/s2,最大静摩擦力等于滑动摩擦力)
将(g=10m/s2,最大静摩擦力等于滑动摩擦力)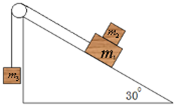
A.和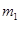 一起沿斜面下滑 一起沿斜面下滑 | B.和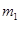 一起沿斜面上滑 一起沿斜面上滑 | C.相对于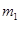 上滑 上滑 | D.相对于 下滑 下滑 |
如图所示,一夹子夹住木块,在力F作用下向上提升.夹子和木块的质量分别为m、M,夹子与木块两侧间的最大静摩擦力均为f.若木块不滑动,力F的最大值是
A. | B. |
C. -(m+M)g -(m+M)g | D. + (m+M)g + (m+M)g |
某游乐场开发了一个名为“翻天滚地”的游乐项目。原理图如图所示:一个 圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,B点为圆轨道最低点,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点。让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程,不考虑空气阻力,球视为质点。那么以下说法中正确的是
圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,B点为圆轨道最低点,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点。让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程,不考虑空气阻力,球视为质点。那么以下说法中正确的是
A.要使球能从C点射出后能打到垫子上,则球经过C点时的速度至少为 |
| B.球从A到B的过程中重力的功率先减小后增大 |
C.若球从C点射出后恰好能打到垫子的M端,则球经过C点时对管外壁压力大小为 |
| D.要使球能通过C点落到垫子上,球离A点的最大高度是5R |
如图所示,乘坐游乐园的翻滚过山车时,质量为m的人随车在竖直平面内旋转,下列说法正确的是
| A.车在最高点时人处于倒坐状态,全靠保险带拉住,没有保险带,人就会掉下来 |
| B.人在最高点时对座位仍可能产生压力 |
| C.人在最低点时对座位的压力等于mg |
| D.人在最低点时对座位的压力大于mg |
一质量为m的物块在倾角为 的足够长斜面上匀减速下滑.现对物块施加一个竖直向下的恒力F,如图所示.则物块减速为零的时间将
的足够长斜面上匀减速下滑.现对物块施加一个竖直向下的恒力F,如图所示.则物块减速为零的时间将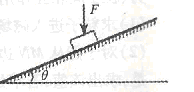
| A.变大 | B.变小 | C.不变 | D.不能确定 |
如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距L=1 m,导轨平面与水平面成θ=37°角,下端连接阻值R=2 Ω的电阻.匀强磁场方向与导轨平面垂直.质量m=0.2 kg、电阻r=1 Ω的金属棒ab放在两导轨上.棒与导轨垂直并保持良好接触,它们之间的动摩擦因数μ=0.25(设最大静摩擦力大小等于滑动摩擦力大小).当金属棒由静止下滑60 m时速度达到稳定,电阻R消耗的功率为8 W,金属棒中的电流方向由a到b,则下列说法正确的是(g=10 m/s2,sin 37°=0.6,cos 37°=0.8)( )
| A.金属棒沿导轨由静止开始下滑时,加速度a的大小为 4 m/s2 |
| B.金属棒达到稳定时速度v的大小为10 m/s |
| C.磁场方向垂直导轨平面向上,磁感应强度B的大小为 0.4 T |
| D.金属棒由静止到稳定过程中,电阻R上产生的热量为 25.5 J |






