题目内容
(6分) 如图所示, 木板A质量mA=1 kg, 足够长的木板B质量mB=4 kg, 质量为mC=1kg的木块C置于木板B上, 水平面光滑, B、C之间有摩擦,开始时B、C均静止,现使A以v0=12 m/s的初速度向右运动, 与B碰撞后以4 m/s速度弹回. 求: 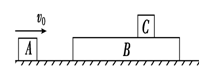
(1)B运动过程中的最大速度大小.
(2)C运动过程中的最大速度大小.
(1)4 m/s.;(2)3.2 m/s.
解析试题分析:(1)A与B碰后瞬间, C的运动状态未变, B速度最大. 由A、B系统动量守恒(取向右为正方向)有: mAv0+0=-mAvA+mBvB
代入数据得: vB=4 m/s.
(2)B与C相互作用使B减速、C加速, 由于B板足够长, 所以B和C能达到相同速度, 二者共速后, C速度最大, 由B、C系统动量守恒, 有
mBvB+0=(mB+mC)vC,代入数据得: vC=3.2 m/s.
考点:动量守恒定律的应用。

练习册系列答案
相关题目
(1)如果一个电子的德布罗意波长和一个中子的相等,则它们的________也相等.
| A.速度 | B.动能 | C.动量 | D.总能量 |

(3)如图所示,进行太空行走的宇航员A和B的质量分别为80 kg和100 kg,他们携手远离空间站,相对空间站的速度为0.1 m/s.A将B向空间站方向轻推后,A的速度变为0.2 m/s,求此时B的速度大小和方向.


 的人以对地速度v从A船跳上B船,再从B船跳回A船,经过几次后人停在B船上。不计水的阻力,则( )
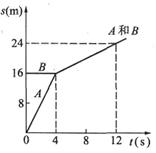
的人以对地速度v从A船跳上B船,再从B船跳回A船,经过几次后人停在B船上。不计水的阻力,则( ) 。若不计碰撞时间,它们碰撞前后的位移图像如图所示。碰撞前B的质量为
。若不计碰撞时间,它们碰撞前后的位移图像如图所示。碰撞前B的质量为 ;碰撞过程中A物体的动量改变量是
;碰撞过程中A物体的动量改变量是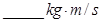 。
。