题目内容
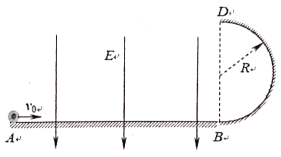
【题目】如图所示，OP为固定的水平轨道，ON段光滑，NP段粗糙，NP段长为L＝l.5m，一轻弹簧一端固定在轨道左侧O点的竖直挡板上，另一端自然伸长时在N点，P点右侧有一与水平方向成θ＝37角的足够长的传送带PQ与水平面在P点平滑连接，传送带逆时针转动的速率恒为v＝3m/s．现用力将质量m＝2kg小物块A缓慢向左压缩弹簧至M点，此时弹簧的弹性势能EP＝3lJ，然后由静止释放，运动到P点与一个和A相同物块B发生碰撞，时间极短，碰撞时无机械能损失．A与NP段间的动摩擦因数
1＝0.2，B与传送带间的动摩擦因数2＝0.25，重力加速度g取10m/s2，
，求：
（1）第一次碰撞前瞬间A的速度大小；
（2）第一次碰撞后A、B的速度大小；
（3）从A、B第一次碰撞后到第二次碰撞间经历的时间t．（最终结果可用根号表示）
【答案】（1）5m/s；（2）0，5m/s （3）
s.
【解析】
本题考查动量守恒定律和能量守恒定律的应用。
（1）设第一次碰撞前A的速度为v0，从M到P由动能定理可知：
解得：
（2）设第一次碰撞后A、B小球的速度分别为v1、v2，由动量守恒定律和能量守恒可知：
解得：
，
（3）碰后B沿传送带向上匀减速运动到速度为零，加速度大小设为a1，则
解得：
运动的时间为：
位移为：
此后B反向加速，加速度仍为a1，与传送带共速时，加速时间为：
位移为：
接着B以加速度a2继续加速运动直到与A再次碰撞
解得：
运动的总时间：
练习册系列答案
相关题目
