Question

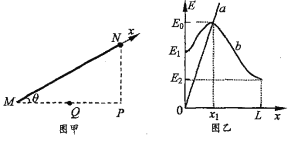
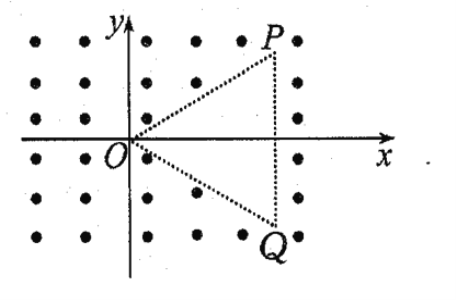
【题目】如图所示，在xOy平面内，有边长为L的等边三角形区域OPQ，PQ边与x轴垂直，在三角形区域以外，均存在着磁感应强度大小为B，方向垂直于纸面向外的匀强磁场，三角形OPQ区域内无磁场分布。现有质量为m，带电量为+q的粒子从O点射入磁场，粒子重力忽略不计。

(1)若要使该粒子不出磁场，直接到达P点，求粒子从O点射入的最小速度的大小和方向；

(2)若粒子从O点以初速度沿y轴正方向射入，能再次经过O点，试画出粒子运动的轨迹图并求该粒子从出发到再次过O点所经历的时间。

Answer 1

【答案】(1) , 方向垂直于OP向上或与y轴正半轴成30°角斜向左上。

(2)

【解析】

(1)粒子运动轨迹如图所示：

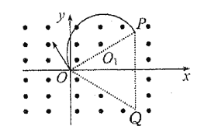
当初速度v1垂直于OP射入磁场时，粒子射入速度最小。由几何关系得：

由牛顿第二定律得：

解得：

方向垂直于OP向上或与y轴正半轴成30°角斜向左上。

(2)若粒子从0点以初速度沿y轴正方向射入

由牛顿第二定律得：

解得：

粒子运动轨迹如图所示：

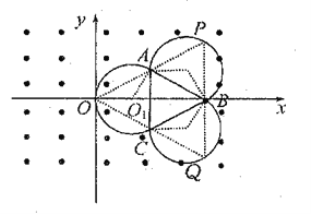
粒子从O运动至A点出磁场进入三角形区域，由几何关系得：

圆心角，运动时间：

粒子从A到B做匀速直线运动，运动时间：

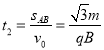
由运动轨迹可知，粒子可以回到O点，所用时间为：