题目内容
如图所示，一固定在竖直平面内的光滑半圆形轨道ABC，半径为R=0.5m，轨道在C处与粗糙的水平面相切，在D处有一质量m=1kg的小物体压缩着弹簧，在弹力的作用下以一定的初速度水平向左运动，物体与水平面间的动摩擦因数为0.25，物体通过C点后进入圆轨道运动，恰好能通过半圆轨道的最高点A，最后又落回水平面上的D点（g=10m/s2,不计空气阻力），
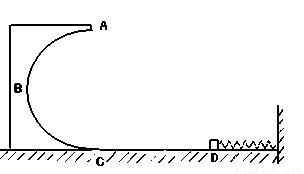
求：(1)物体到C点时的速度 ;
（2）弹簧对物体做的功。
【答案】
（1）5m/s（2）15J
【解析】
试题分析：（1）物体恰好通过A点有：mg=m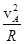
得vA=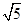
m/s
物块由C到A过程有：mg2R+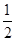
mvA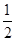2=mvC2
vC=5m/s
(2) 物体从A到D做平抛运动有2Ｒ=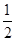gt2
所以 SCD=vAt=1m
物块由D到C过程有W-μmg SCD =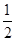mvC2
W=15J
考点：此题考查的物理模型有圆周运动、平抛运动；考查的规律是牛顿第二定律及机械能守恒定律。
练习册系列答案
相关题目
（2006?甘肃）如图所示，一固定在竖直平面内的光滑的半圆形轨道ABC，其半径R=0.5m，轨道在C处与水平地面相切，在C处放一小物块，给它一水平向左的初速度v0=5m/s，结果它沿CBA运动，通过A点，最后落在水平地面上的D点，求C、D间的距离x．取重力加速度g=10m/s2．
如图所示，一固定在竖直平面内的光滑半圆形轨道ABC在C处与水平地面相切，轨道半径R=0.5m．在与C相距x=3m的O点放一小物体，物体与水平面问的动摩擦因数μ=0.4． 现给物体一水平向左的初速度v0，结果它沿OCBA 运动通过A点，最后落在水平地面上的D点（图中未画出），C、D问的距离s=l m，求物体的初速度秒v0的大小．（取重力加速度g=l0m/s2）
如图所示，一固定在竖直平面内的光滑的半圆形轨道ABC，其半径R=0.5m，轨道在C处与水平地面相切．在C处放一小物块，给它一水平向左的初速度，结果它沿CBA运动，小物块恰好能通过最高点A，最后落在水平面上的D点，（取g=10m/s2）求：
如图所示，一固定在竖直平面内的光滑的半圆形轨道ABC，其半径R=2.5m，轨道在C处与水平地面相切．在C处放一小球，给它一水平向左的初速度，结果它沿CBA运动，恰能通过A点，最后落在水平面上的D点，（g取10m/s2）
如图所示，一固定在竖直平面内的光滑的半圆形轨道ABC，其半径R=0.5m，轨道在C处与水平地面相切．在C处放一质量m=1kg的小物块，给它一水平向左的初速度v0=5m/s，结果它沿CBA运动，通过最高点A点后落在水平面上．求：