题目内容
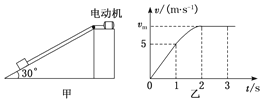
【题目】如图甲所示，电动机通过绕过光滑定滑轮的细绳与放在倾角为
的光滑斜面上的物体相连，启动电动机后物体沿斜面上升；在
时间内物体运动的
图象如图乙所示，其中除
时间段图象为曲线外，其余时间段图象均为直线，1s后电动机的输出功率保持不变；已知物体的质量为2kg，重力加速度
则下列计算不正确的是
A. 1s后电动机的输出功率P为100W
B. 物体运动的最大速度
为10
C. 在
s内电动机所做的功为25J
D. 在
s内电动机所做的功为250J
【答案】C
【解析】
根据图乙得出
的加速度，再根据牛顿第二定律得出牵引力
，最后由
算出电动机的输出功率；
当加速度为0时，物体运动速度最大，根据二力平衡求出此时牵引力
，结合算出最大速度；
内根据运动学公式及动能定理算出电动机所做的功；
内，根据电动机功率变，结合
算出。
A、设物体质量为m，由题图乙可知，在
s时间内，物体做匀加速直线运动的加速度大小为a，1s末物体的速度大小达到
，此过程中，设细绳拉力的大小为
，则根据运动学公式和牛顿第二定律可得：
，
，由图象可知，
，由功率公式
，联立解得：在1s末电动机输出功率为：
，故A正确.
B、当物体达到最大速度
后，细绳的拉力大小
，由牛顿第二定律和功率的公式可得：
，由
解得
，故B正确.
C、s内，物体的位移为x，电动机做的功为
，则由运动学公式得：
由动能定理得：
，联立解得：
，故C错误.
D、在时间t=3s内电动机做的功为W，则：
，联立解得：
故D正确.
故选C.
练习册系列答案
相关题目
