题目内容
【题目】如图所示,真空中一平面直角坐标系xOy内,存在着两个边长为L的正方形匀强电场区域I、II和两个直径为L的圆形匀强磁场区域III,IV.电场的场强大小均为E,区域I的场强方向沿x轴正方向,其下边界在x轴上,右边界刚好与区域III的边界相切;区域II的场强方向沿y轴正方向,其上边界在x轴上,左边界刚好与区域仅的边界相切.磁场的磁感应强度大小均为![]() ,区域III的圆心坐标为(0,
,区域III的圆心坐标为(0,![]() )、磁场方向垂直于xOy平面向外;区域IV的圆心坐标为(0,-
)、磁场方向垂直于xOy平面向外;区域IV的圆心坐标为(0,-![]() ),磁场方向垂直于xOy平面向里.两个质量均为m、电荷量均为q的带正电粒子M、N,在外力约束下静止在坐标分别为(
),磁场方向垂直于xOy平面向里.两个质量均为m、电荷量均为q的带正电粒子M、N,在外力约束下静止在坐标分别为(![]() ,
,![]() )、(
)、(![]() ,
,![]() )的两点.在Y轴的正半轴(坐标原点除外)放置一块足够长的感光板,板面垂直于xOy平面.将粒子M、N由静止释放,它们最终打在感光板上并立即被吸收.不计粒子的重力.求:
)的两点.在Y轴的正半轴(坐标原点除外)放置一块足够长的感光板,板面垂直于xOy平面.将粒子M、N由静止释放,它们最终打在感光板上并立即被吸收.不计粒子的重力.求:
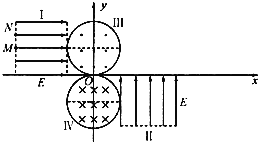
(1)粒子离开电场I时的速度大小.
(2)粒子M击中感光板的位置坐标.
(3)粒子N在磁场中运动的时间.
【答案】(1)![]() (2)(2L,0)(3)
(2)(2L,0)(3)![]()
【解析】
(1)粒子在区域Ⅰ中运动,由动能定理得:![]()
计算得出![]() .
.
(2)粒子在磁场中做匀速圆周运动,由牛顿第二定律得:![]()
因![]()
故得![]()
因M运动的轨道半径与磁场区域的半径相同,故M在磁场Ⅲ中运动四分之一周期后经过原点进入磁场Ⅳ,再运动四分之一周期后平行于x轴正方向离开磁场,然后进入电场Ⅱ做类平抛运动;假设M射出电场后再打在x轴的感光板上,则:
M在电场中运动时间![]()
沿电场力位移![]() ;
;
所以假设成立,运动轨迹如右图所示.沿电场方向的速度![]()
速度偏向角的正切![]()
设出电场后沿x轴方向的位移为x1,则![]() ,所以
,所以![]() ;
;
M击中感光板的横坐标为![]() ,位置坐标为(2L,0);
,位置坐标为(2L,0);
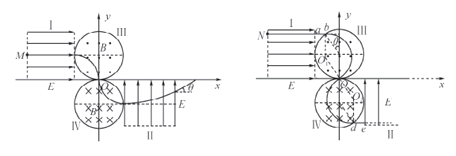
(3)N做圆周运动的轨道半径与磁场区域的半径相同,分析可得N将从b点进入磁场,由坐标原点O离开磁场Ⅲ进入磁场,然后从d点离开磁场Ⅳ,其部分轨迹如右图所示;
在磁场Ⅲ中,由几何关系得: 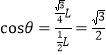 ;所以θ=300;
;所以θ=300;
圆弧对应的圆心角![]()
粒子在运动的周期![]()
所以粒子在磁场Ⅲ中运动的时间![]()
由对称关系得粒子在磁场Ⅲ、Ⅳ中运动时间相同,故粒子在磁场中运动的时间为:![]()

 阅读快车系列答案
阅读快车系列答案