题目内容
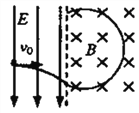
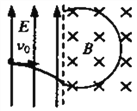
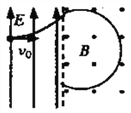
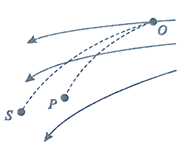
【题目】如图所示,OPQ为等腰直角三角形,S为直角边OQ的中点,OS=l。在三角形OPQ区域内有磁感应强度大小为B、方向垂直纸面向里的匀强磁场,还有电场强度大小为E、方向平行于纸面的匀强电场(图中未画出),一比荷(带电粒子的电荷量和质量的比值)为![]() 的带正电的粒自S点沿平行于OP的方向人射,粒子沿直线通过三角形OPQ区域,不计带电粒子的重力。求
的带正电的粒自S点沿平行于OP的方向人射,粒子沿直线通过三角形OPQ区域,不计带电粒子的重力。求
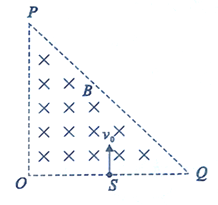
(1)粒子自S点入射进入场区的速度大小v0和三角形区域内电场强度的方向。
(2)若仅撤去电场,粒子仍以原速度自S点射入磁场,判断粒子从哪边射出,并求粒子射出磁场的点离P点的距离。
(3)若仅撒去磁场,粒子仍以原速度自S点射入电场,求粒子在电场中的运动时间
【答案】(1)![]() , 场强方向水平向右(2)(2-
, 场强方向水平向右(2)(2- ![]() )l (3)
)l (3)![]()
【解析】(1)正粒子在场区受力平衡:qE =q v0B
解得粒子自S点入射进入场区的速度大小: ![]()
根据左手定则判断,正粒子在匀强磁场受洛伦兹力方向水平向左,根据正粒子所受电场力的方向与场强的方向相同,可知场强方向水平向右
(2)设正粒子在磁场中做匀速圆周运动运动的半径为R,则![]()
解得半径R=2l
如图甲所示,粒子从OP边界上的A点射出则OC2+OA2=CA2
解得OA=![]() l
l
出射点离P点的距离AP=(2- ![]() )l
)l
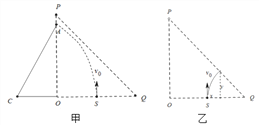
(3)如图乙所示。粒子在电场中沿初速度方向做匀速直线运动:y=v0t
粒子沿电场的方向做匀加速直线运动:x=![]() at2
at2
粒子在电场中的加速度大小为![]()
由几何关系:y + x =l
联立得 ![]()
解得粒子在电场中的运动时间![]()

练习册系列答案
相关题目