题目内容
16. 如图所示,质量为4m的足够长木板C静止在光滑水平面上,质量均为m的两个小物体A、B放在C的左端,A、B间距离为d,现同时对A、B施加水平向右的瞬时冲量而使之分别获得初速度v0和3v0,A、B始终未滑离C,若A、B与C之间的动摩擦因数分别为μ和3μ,求:
如图所示,质量为4m的足够长木板C静止在光滑水平面上,质量均为m的两个小物体A、B放在C的左端,A、B间距离为d,现同时对A、B施加水平向右的瞬时冲量而使之分别获得初速度v0和3v0,A、B始终未滑离C,若A、B与C之间的动摩擦因数分别为μ和3μ,求:(1)运动过程中A的最小速度;
(2)最终A、B相距多远.
(3)整个过程中A与C及B与木板C因摩擦所产生的热量之比.
分析 (1)对A、B施加水平向右的瞬时冲量,使之分别获得初速度v0和3v0后,A、B都向右做减速运动,B向右做加速运动,当A与C的速度相同后,AC一起向右做加速运动,那么AC相对静止时A的速度最小.根据动量守恒定律和动量定理分别对A、长木板研究,求出运动过程中A的最小速度.
(2)根据牛顿第二定律分别求出AC相对静止前后三个物体的加速度大小,由速度位移公式求出从开始运动到三个物体均相对静止时相对于地面的位移,再求出A与B最终相距的距离.
(3)结合运动学公式求出整个过程中C的位移大小,从而得出A、B相对C滑动的位移大小,结合摩擦产生的热量与相对位移的关系求出产生的热量之比.
解答 解:(1)当A、C速度相等时,A的速度最小,
设经过t时间,A与C相对静止,共同速度为vAC,此时B的速度为vB,规定向右为正方向,由动量守恒得:
mv0+3mv0=(m+4m)vAC+mvB
根据动量定理,
对A:-μmgt=m(vAC-v0)
对C:(μmg+3μmg)t=4mvAC
联立以上三式解得:vAC=0.5v0,vB=1.5v0.
(2)AC相对静止前,AB做匀减速运动,C做匀加速运动,三个物体的加速度分别为:
${a}_{A}=\frac{μmg}{m}=μg$,${a}_{B}=\frac{3μmg}{m}=3μg$,${a}_{C}=\frac{μmg+3μmg}{4m}=μg$,
AC相对静止后,AC做匀加速运动,B做匀减速运动,三个物体的加速度分别为:
${a}_{A}′={a}_{C}′=\frac{3μmg}{5m}=\frac{3μg}{5}$,
aB′=aB=3μg,
最终三个物体一起做匀速直线运动.
从开始运动到三个物体都相对静止,A、B相对于地的位移分别为:
${s}_{A}=\frac{{{v}_{0}}^{2}-{{v}_{AC}}^{2}}{2{a}_{A}}+\frac{{v}^{2}-{{v}_{AC}}^{2}}{2{a}_{A}′}$=$\frac{29{{v}_{0}}^{2}}{54μg}$,
${s}_{B}=\frac{(3{v}_{0})^{2}-{v}^{2}}{2{a}_{B}}$=$\frac{77{{v}_{0}}^{2}}{54μg}$,
规定向右为正方向,对三者组成的系统运用动量守恒得:
mv0+3mv0=(m+m+4m)v
解得:v=$\frac{2}{3}$v0.
所以A与B最终相距为:△s=d+sB-sA=d+$\frac{8{{v}_{0}}^{2}}{9μg}$.
(3)C在整个过程中的位移为:${s}_{C}=\frac{{{v}_{AC}}^{2}}{2{a}_{C}}+\frac{{v}^{2}-{{v}_{AC}}^{2}}{2{a}_{C}′}$=$\frac{31{{v}_{0}}^{2}}{108μg}$,
可知A相对C滑动的位移为:$△{x}_{A}={s}_{A}-{s}_{C}=\frac{{{v}_{0}}^{2}}{4μg}$,
B相对C滑动的位移为:△xB=sB-sC=$\frac{41{{v}_{0}}^{2}}{36μg}$.
QA=μmg△xA,QB=3μmg△xB,
解得:$\frac{{Q}_{A}}{{Q}_{B}}$=$\frac{3}{41}$.
答:(1)运动过程中A的最小速度为0.5v0;
(2)最终A、B相距d+$\frac{8{{v}_{0}}^{2}}{9μg}$.
(3)整个过程中A与C及B与木板C因摩擦所产生的热量之比为3:41.
点评 本题综合考查了动量守恒定律、动量定理、牛顿运动定律和运动学公式,运动过程比较复杂,研究对象比较多,按程序法进行分析,理清物体在整个过程中的运动规律,选择合适的规律进行求解.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案| A. | 当加速度与速度同向时,物体做加速直线运动 | |
| B. | 当加速度与速度同向时,物体做减速直线运动 | |
| C. | 当加速度与速度反向时,物体做加速直线运动 | |
| D. | 当加速度与速度反向时,物体做减速直线运动 |
 如图,物体在恒力F作用下沿曲线从A运动到B.这时,如突然使它所受力反向,大小不变,即由F变为-F.在此力作用下,物体以后的运动情况,下列说法正确的是( )
如图,物体在恒力F作用下沿曲线从A运动到B.这时,如突然使它所受力反向,大小不变,即由F变为-F.在此力作用下,物体以后的运动情况,下列说法正确的是( )| A. | 物体可能沿曲线Ba运动 | B. | 物体可能沿曲线Bb运动 | ||
| C. | 物体可能沿曲线Bc运动 | D. | 物体可能沿B返回A |
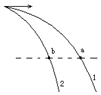 小球两次从同一位置水平抛出,运动轨迹如图所示.轨迹上a、b两点在同一水平线上.设小球从抛出到运动到a、b两点运动的时间分别为t1、t2,则( )
小球两次从同一位置水平抛出,运动轨迹如图所示.轨迹上a、b两点在同一水平线上.设小球从抛出到运动到a、b两点运动的时间分别为t1、t2,则( )| A. | t1=t2 | B. | t1>t2 | C. | t1<t2 | D. | 无法判断 |
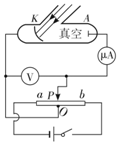
| A. | 光电效应中,从金属逸出的光电子就是光子 | |
| B. | 图中为使电流表的示数减小为零应将触头P向b端移动 | |
| C. | 用频率为ν1的光照射光电管,改变滑片位置当电流表示数减为零时电压表示数U1,用频率为ν2的光照射光电管,电流表示数减为零时电压表示数U2,可得普朗克常量h=$\frac{{e({U_1}-{U_2})}}{{{ν_1}-{ν_2}}}$(e为电子的电量) | |
| D. | 光电效应说明光具有粒子性康普顿效应说明光具有波动性 |
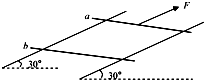 如图所示,两条足够长的平行金属导轨倾斜放置(导轨电阻不计),倾角为30°,导轨间距为0.5m,匀强磁场垂直导轨平面向下,B=0.2T,两根材料相同的金属棒a、b与导轨构成闭合回路,a、b金属棒的质量分别为3kg、2kg,两金属棒的电阻均为R=1Ω,刚开始两根金属棒都恰好静止,假设最大静摩擦力近似等于滑动摩擦力.现对a棒施加一平行导轨向上的恒力F=60N,经过足够长的时间后,两金属棒都达到了稳定状态.求:
如图所示,两条足够长的平行金属导轨倾斜放置(导轨电阻不计),倾角为30°,导轨间距为0.5m,匀强磁场垂直导轨平面向下,B=0.2T,两根材料相同的金属棒a、b与导轨构成闭合回路,a、b金属棒的质量分别为3kg、2kg,两金属棒的电阻均为R=1Ω,刚开始两根金属棒都恰好静止,假设最大静摩擦力近似等于滑动摩擦力.现对a棒施加一平行导轨向上的恒力F=60N,经过足够长的时间后,两金属棒都达到了稳定状态.求: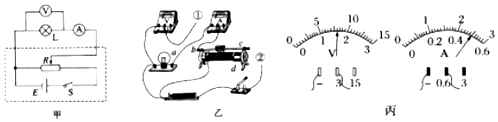 某同学做测绘“2.5V,0.5A”小灯泡的伏安特性曲线的实验,实验电路图如图甲所示,图乙为实物连线图.
某同学做测绘“2.5V,0.5A”小灯泡的伏安特性曲线的实验,实验电路图如图甲所示,图乙为实物连线图.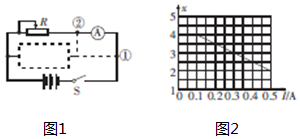 某同学要测定三节干电池组成电池组的电动势和内阻,实验室中提供如下器材:
某同学要测定三节干电池组成电池组的电动势和内阻,实验室中提供如下器材: