题目内容
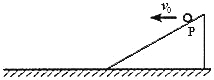
【题目】如图所示,M、N为两平行金属板,期间电压为U。质量为m、电荷量为+q的粒子,从M板由静止开始经电场加速后,从N板上的小孔射出,并沿与ab垂直的方向由d点进入△abc区域,不计粒子重力,一直bc=l,∠c=60°,∠b=90°,ad= ![]() 。
。
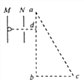
(1)求粒子从N板射出时的速度v0;
(2)若abc区域内存在垂直纸面向外的匀强磁场,要使粒子不从bc边界射出,则磁感应强度应为多大?
(3)若abc区域内存在平行纸面且垂直bc方向的匀强电场,要使粒子不从ac边界射出,电场强度应为多大?
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】(1)带电粒子在MN间加速:
![]()
![]()
(2)带电粒子在磁场中做匀速圆周运动,磁感应强度越大,半径越小;当磁感应强度最小时,恰不从ac边界射出粒子到达ac边界时,速度方向沿ac方向。设轨迹圆的最小半径为r,根据![]()
由几何关系: ![]()
解得![]() ,所以
,所以![]()
(3)带电粒子在电场中做类平抛运动,电场强度最小为E0时,粒子运动到ac界面的速度方向沿ac方向,设ab和bc方向的位移大小分别为x、y,到达界面时沿ab方向分速度大小为vy:
x=v0t
![]()
![]()
![]()
解得![]()
粒子到达ac界面的速度的大小为v
![]()
![]()
解得![]() ,所以
,所以![]()

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目