题目内容
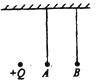
【题目】如图所示,质量为M的导体棒ab,垂直放在相距为l 的平行光滑金属导轨上,导轨平面与水平面的夹角为θ,并处于磁感应强度大小为B方向垂直于导轨平面向上的匀强磁场中,左侧是水平放置间距为d的平行金属板,R和Rx分别表示定值电阻和滑动变阻器的阻值,不计其他电阻.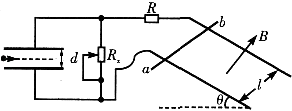
(1)调节Rx=R,释放导体棒,当棒沿导轨匀速下滑时,求通过棒的电流I及棒的速率v.
(2)改变Rx , 待棒沿导轨再次匀速下滑后,将质量为m带电量为+q的微粒水平射入金属板间,若它能匀速通过,求此时的Rx .
【答案】
(1)
解:导体棒匀速下滑时,Mgsinθ=BIl①
I= ![]() ②
②
设导体棒产生的感应电动势为E0
E0=BLv③
由闭合电路欧姆定律得:
I= ![]() ④
④
联立②③④,得
v= ![]() ⑤
⑤
(2)
解:改变Rx由②式可知电流不变.设带电微粒在金属板间匀速通过时,板间电压为U,电场强度大小为E
U=IRx⑥
E= ![]() ⑦
⑦
mg=qE⑧
联立②⑥⑦⑧,得
Rx= ![]() ⑨
⑨
【解析】由电磁感应定律求电动势E=BLv、闭合电路欧姆定律求电流I= ![]() ,由导体棒受力平衡求速度,由带电粒子的匀速通过电容器求电压,结合闭合电路求速度.
,由导体棒受力平衡求速度,由带电粒子的匀速通过电容器求电压,结合闭合电路求速度.
【考点精析】本题主要考查了电磁感应与电路的相关知识点,需要掌握用法拉第电磁感应定律和楞次定律确定感应电动势的大小和方向;画等效电路;运用全电路欧姆定律,串并联电路性质,电功率等公式联立求解才能正确解答此题.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目