题目内容
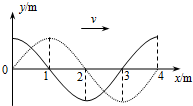如图所示，实线为一列沿x轴正方向传播的简谐横波在t=0时刻的波形，虚线是该波在t=0.20s时刻的波形，则此列波的周期可能（ ）| A、0.16s | B、0.20s | C、0.32s | D、0.40s |
分析：波沿x轴正方向传播，传播的最短距离为1m，根据波的周期性：相隔整数倍周期的时间，波形相同，根据时间与周期关系的通项，求出周期．
解答：解：设波的周期为T．
波沿x轴正方向传播，则t=（n+
）T，得到T=
=
s （n=0，1，2，…）
当n=1时，T=0.16s
由于n是整数，T不可能等于0.20s、0.32s、0.40s．故A正确，BCD错误．
故选：A
波沿x轴正方向传播，则t=（n+
| 1 |
| 4 |
| 4t |
| 4n+1 |
| 0.8 |
| 4n+1 |
当n=1时，T=0.16s
由于n是整数，T不可能等于0.20s、0.32s、0.40s．故A正确，BCD错误．
故选：A
点评：本题是波动图象中典型的问题，要根据波的周期性研究时间与周期的关系．若波的传播方向未知，还要考虑波的双向性．
练习册系列答案
相关题目
如图所示，实线为一列横波在t时刻的波形图，虚线为经过△t=0.2s时的波形图．已知这列波的波长为2m，那么（ ）
如图所示，实线为一列横波某时刻的图象，这列波的传播速度为0.25m/s，经过时间1s后的波形为虚线所示．那么这列波的传播方向与在这时间内质点P所通过的路程是（ ）?
如图所示，实线为一列简谐波在t=0时刻的波形，a点振动方向沿y轴正向，经t=1s波形为图中虚线，求波的传播速度．
如图所示，实线为一列简谐横波在t1=0时刻的波形，虚线是它在t2=0.5s时刻的波形．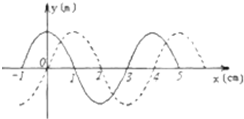
如图所示，实线为一列简谐波在t=0时刻的波形，虚线表示经过△t=0.2s后它的波形图象，已知T＜△t＜2T（T表示周期），则这列波传播速度的可能值v=