题目内容
 如图所示,实线为一列简谐横波在t1=0时刻的波形,虚线是它在t2=0.5s时刻的波形.
如图所示,实线为一列简谐横波在t1=0时刻的波形,虚线是它在t2=0.5s时刻的波形.(1)如果这列波的速度为54m/s,那么这列波向哪个方向传播?
(2)若2T<0.5s<3T,而且波向左传播,则在0.5s后,x=5m处的质点在哪些时刻出现波峰?
分析:(1)根据公式s=υ(t2-t1),求出这列波在0.5s内传播的距离,分析此距离与波长的关系,结合波形判断波的传播方向.
(2)若2T<0.5s<3T,而且波向左传播,得到0.5=(2+
)T,求出周期T.x=5m处的质点在t2时刻后出现波峰需要经过时间为 t=(n+
)T.(n=0,1,2,…),即可得到相应的时刻.
(2)若2T<0.5s<3T,而且波向左传播,得到0.5=(2+
| 5 |
| 8 |
| 3 |
| 4 |
解答:解:(1)波在0.5 s内传播的距离为:s=υt2=54×0.5 m=27m=(3+
)λ
所以根据波形平移法得知,该波向右传播.
(2)波向左传播,且2T<0.5s<3T,说明0.5=(2+
)T
则 T=
s
在0.5s时刻x=5m处的质点振动方向向下,故x=5m处的质点在t2时刻后出现波峰需要经过(n+
)T的时间.
所以x=5m处的质点出现波峰的时刻为 t=t2+(n+
)T=0.5s+(n+
)×
s=(
n+
)s,(n=0,1,2,…).
答:(1)如果这列波的速度为54m/s,那么这列波向右传播.
(2)若2T<0.5s<3T,而且波向左传播,则在0.5s后,x=5m处的质点在出现波峰的时刻为t=(
n+
)s,(n=0,1,2,…).
| 3 |
| 8 |
所以根据波形平移法得知,该波向右传播.
(2)波向左传播,且2T<0.5s<3T,说明0.5=(2+
| 5 |
| 8 |
则 T=
| 4 |
| 21 |
在0.5s时刻x=5m处的质点振动方向向下,故x=5m处的质点在t2时刻后出现波峰需要经过(n+
| 3 |
| 4 |
所以x=5m处的质点出现波峰的时刻为 t=t2+(n+
| 3 |
| 4 |
| 3 |
| 4 |
| 4 |
| 21 |
| 4 |
| 21 |
| 9 |
| 14 |
答:(1)如果这列波的速度为54m/s,那么这列波向右传播.
(2)若2T<0.5s<3T,而且波向左传播,则在0.5s后,x=5m处的质点在出现波峰的时刻为t=(
| 4 |
| 21 |
| 9 |
| 14 |
点评:根据波传播的距离与波长关系,是判断波的传播方向常用的方法.对于波动图象往往要抓住波的周期性进行分析,要防止漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,实线为一列横波在t时刻的波形图,虚线为经过△t=0.2s时的波形图.已知这列波的波长为2m,那么( )
如图所示,实线为一列横波在t时刻的波形图,虚线为经过△t=0.2s时的波形图.已知这列波的波长为2m,那么( ) 如图所示,实线为一列横波某时刻的图象,这列波的传播速度为0.25m/s,经过时间1s后的波形为虚线所示.那么这列波的传播方向与在这时间内质点P所通过的路程是( )?
如图所示,实线为一列横波某时刻的图象,这列波的传播速度为0.25m/s,经过时间1s后的波形为虚线所示.那么这列波的传播方向与在这时间内质点P所通过的路程是( )? 如图所示,实线为一列简谐波在t=0时刻的波形,a点振动方向沿y轴正向,经t=1s波形为图中虚线,求波的传播速度.
如图所示,实线为一列简谐波在t=0时刻的波形,a点振动方向沿y轴正向,经t=1s波形为图中虚线,求波的传播速度.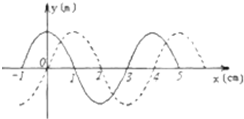 如图所示,实线为一列简谐波在t=0时刻的波形,虚线表示经过△t=0.2s后它的波形图象,已知T<△t<2T(T表示周期),则这列波传播速度的可能值v=
如图所示,实线为一列简谐波在t=0时刻的波形,虚线表示经过△t=0.2s后它的波形图象,已知T<△t<2T(T表示周期),则这列波传播速度的可能值v=