题目内容
如图,竖直环A半径为r，固定在木板B上，木板B放在水平 地面上，B的左右两侧各有一档板固定在地上，B不能左右运动，在环的最低点静放有一小球C，A．B．C的质量均为m。给小球一水平向右的瞬时速度V，小球会在环内侧做圆周运动，为保证小球能通过环的最高点，且不会使环在竖直方向上跳起，（不计小球与环的摩擦阻力），瞬时速度必须满足
A．最小值 
B．最大值
C．最小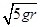值
D．最大值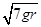
CD
解析试题分析：据题意，先假设小球到达最高点时，小球和环之间没有相互作用力，则小球做圆周运动的向心力有小球的重力提供，则有：mg=mv2/r，则v=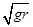
,那么小球在最低点时的速度由：mv2/2+mg2r=mV2/2得V= 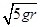，C选项正确；当小球运动到最高点时，为不让环在竖直方向跳起，需要满足：环受到的支持力N和环、B木板的重力相等，即N=2mg，对小球则有N+mg=mv2/2，那么v= 
，则小球在最低点的速度由：mv2/2+mg2r=mV2/2得V=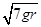，所以C、D选项正确。
考点：本题考查圆周运动问题的分析和向心力的计算、机械能守恒定律的应用。
在如图所示的装置中，木块 B 与水平面间的接触面是光滑的，子弹 A 沿水平方向射入木块后并留在木块内，将弹簧压缩到最短。现将木块、弹簧、子弹合在一起作为研究对象，则此系统在从子弹开始射入到弹簧压缩到最短的过程 中
| A．动量守恒，机械能守恒 |
| B．动量不守恒，机械能不守恒 |
| C．动量守恒，机械能不守恒 |
| D．动量不守恒，机械能守恒 |
B．
C．
D．h如图所示，小车与木箱紧挨着静止在光滑的水平冰面上，现有一男孩站在小车上用力向右迅速推出木箱，关于上述过程，下列说法中正确的是
| A．男孩、小车与木箱三者组成的系统机械能增加； |
| B．男孩、小车与木箱三者组成的系统机械能守恒； |
| C．男孩、小车与木箱三者组成的系统动量守恒； |
| D．小车与木箱组成的系统动量守恒。 |
下列说法正确的是（ ）
| A．物体机械能守恒时，一定只受重力作用 |
| B．物体处于平衡状态时机械能一定守恒 |
| C．若物体除受重力外还受到其他力作用，物体的机械能也可能守恒 |
| D．物体的动能和重力势能之和增大，必定有重力以外的其他力对物体做功 |
一根用绝缘材料制成劲度系数为k的轻弹簧，左端固定，右端与质量为m、电荷量为+q的小球相连，静止在光滑绝缘水平面上，当施加一个场强为E水平向右的匀强电场后，小球开始做往复运动。那么( )
| A．小球的运动是简谐振动； |
| B．小球做简谐运动的振幅为2qE/k； |
| C．运动过程中小球的机械能守恒 |
| D．小球从左向右的运动过程中，系统的机械能逐渐增大 |
如右图所示，一轻绳通过无摩擦的小定滑轮O与小球B连接，另一端与套在光滑竖直杆上的小物块A连接，杆两端固定且足够长，物块A由静止从图示位置释放后，先沿杆向上运动。设某时刻物块A运动的速度大小为υA，小球B运动的速度大小为υB，轻绳与杆的夹角为θ。则：
| A．υA＝υBcosθ |
| B．υB＝υAcosθ |
| C．小球B减少的势能等于物块A增加的动能 |
| D．当物块A上升到与滑轮等高时，它的机械能最大 |
如图所示，一根轻杆两端有小球a、b，它们的质量分别是m和2m，杆可绕中心点O自由转动，使杆由水平位置无初速度释放，杆转至竖直位置的过程中
| A．b球的重力势能减少，动能增加，机械能守恒 |
| B．杆对a球做正功 |
| C．杆对b球做正功 |
| D．整个系统的机械能守恒 |