题目内容
【题目】威廉·赫歇尔于1789年发现了土星的两颗卫星——土卫一、土卫二。已知引力常量G=6.67×1011Nm2/kg2。土卫一和土卫二的直径、公转轨道半径和公转周期如下表，若将土星视为质量分布均匀的球体，土卫一、土卫二的运动轨迹可视为圆，则根据下表中的数据可以求出的是（ ）
A.土卫二的公转轨道半径B.土星的平均密度
C.土星的第一宇宙速度D.土卫一的平均密度
【答案】A
【解析】
A．根据开普勒第三定律
题中已知土卫1的公转的轨道半径r1和公转周期T1以及土卫二的公转周期T2，则可求解土卫二的公转轨道半径r2，选项A正确；
BC．根据
题中已知土卫1的公转的轨道半径r1和公转周期T1，可求解土星的质量M，但是土星的半径未知，无法求解土星的密度；由
也不能求解土星的第一宇宙速度，选项BC错误；
D．由题中条件无法求解土卫一的质量m，则无法求解其密度，选项D错误。
故选A。
【题目】如图所示，某实验小组同学利用DIS实验装置研究支架上力的分解，A、B为两个相同的双向力传感器，该型号传感器在受到拉力时读数为正，受到压力时读数为负。A连接质量不计的细绳，可沿固定的板做圆弧形移动；B固定不动，通过光滑铰链连接长0.3 m的杆；将细绳连接在杆右端D点构成支架。保持杆在水平方向，g取10 m/s2，按如下步骤操作：
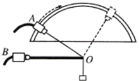
①测量绳子与水平杆的夹角∠AOB＝θ；
②对两个传感器进行调零；
③用另一根绳在D点悬挂一个钩码，记录两个传感器的读数；
④取下钩码，移动传感器A改变θ角。
重复上述实验步骤，得到表格。
F1/N | 1.001 | 0.580 | … | 1.002 | … |
F2/N | －0.868 | －0.291 | … | 0.865 | … |
θ | 30 | 60 | … | 150 | … |
（1）根据表格，A传感器对应的是表中力_____(填“F1”或“F2”)；钩码质量为______kg(保留一位有效数字)。
（2）本实验中多次对传感器进行调零，对此操作说明正确的是________。
A．因为事先忘记调零
B．何时调零对实验结果没有影响
C．为了消除横杆自身重力对结果的影响
D．可以完全消除实验的误差
