题目内容
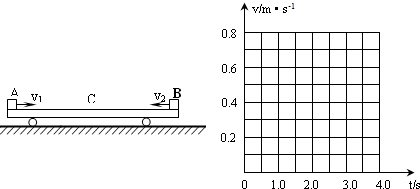
如图所示,质量M=0.6kg的平板小车静止在光滑水平面上.当t=0时,两个质量都是m=0.2kg的小物体A和B(A和B均可视为质点),分别从左端和右端以水平速度v1=5.0m/s和v2=2.0m/s冲上小车,当它们相对于车停止滑动时,没有相碰.已知A、B与车面的动摩擦因数都是0.20,g取10m/s2.求:
(1)A、B在车上都停止滑动时车的速度;
(2)车的长度至少是多少?
(3)在图中所给的坐标系中画出0至4.0s内小车运动的速度--时间图象.
(1)A、B在车上都停止滑动时车的速度;
(2)车的长度至少是多少?
(3)在图中所给的坐标系中画出0至4.0s内小车运动的速度--时间图象.

分析:(1)以A、B和车组成的系统为研究对象,该系统水平方向动量守恒,根据动量守恒定律列方程求解.
(2)对系统运用功能关系,系统克服摩擦力做的功等于系统动能的减少量,列方程求解即可.
(3)第一阶段:A、B同时在车上滑行时,滑块对车的摩擦力均为μmg,方向相反,车受力平衡而保持不动.当B的速度减为0时,此过程结束,第二阶段:B停止运动后,A继续在车上滑动,物体A与车将有共同速度v,最终做匀速直线运动.根据运动学公式结合牛顿第二定律进行求解.
(2)对系统运用功能关系,系统克服摩擦力做的功等于系统动能的减少量,列方程求解即可.
(3)第一阶段:A、B同时在车上滑行时,滑块对车的摩擦力均为μmg,方向相反,车受力平衡而保持不动.当B的速度减为0时,此过程结束,第二阶段:B停止运动后,A继续在车上滑动,物体A与车将有共同速度v,最终做匀速直线运动.根据运动学公式结合牛顿第二定律进行求解.
解答: 解:(1)设A、B相对于车停止滑动时,车的速度为v,根据动量守恒定律得:
解:(1)设A、B相对于车停止滑动时,车的速度为v,根据动量守恒定律得:
m(v1-v2)=(M+2m)v,
解得,v=0.60m/s,方向向右.
(2)设A、B在车上相对于车滑动的距离分别为L1和L2,由功能关系得:
μmgL1+μmgL2=
mv12+
mv22-
(M+2m)v2,
L1+L2=6.8m,故车长最小为6.8m.
(3)车的运动分以下三个阶段:
第一阶段:A、B同时在车上滑行时,滑块对车的摩擦力均为μmg,方向相反,车受力平衡而保持不动.当B的速度减为0时,此过程结束.设这段时间内滑块的加速度为a,根据牛顿第二定律:μmg=ma,a=μg,滑块B停止滑动的时间t=
=1.0s.
第二阶段:B停止运动后,A继续在车上滑动,设到时刻t2物体A与车有共同速度v,则t2=
=2.2s.
第三阶段:t2之后,车以速度v做匀速直线运动到t=4.0s为止.
小车运动的速度--时间图线如图所示.
答:(1)A、B在车上都停止滑动时车的速度为0.60m/s,方向向右.
(2)车的长度至少为6.8m.
(3)速度时间图线如图所示.
 解:(1)设A、B相对于车停止滑动时,车的速度为v,根据动量守恒定律得:
解:(1)设A、B相对于车停止滑动时,车的速度为v,根据动量守恒定律得:m(v1-v2)=(M+2m)v,
解得,v=0.60m/s,方向向右.
(2)设A、B在车上相对于车滑动的距离分别为L1和L2,由功能关系得:
μmgL1+μmgL2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
L1+L2=6.8m,故车长最小为6.8m.
(3)车的运动分以下三个阶段:
第一阶段:A、B同时在车上滑行时,滑块对车的摩擦力均为μmg,方向相反,车受力平衡而保持不动.当B的速度减为0时,此过程结束.设这段时间内滑块的加速度为a,根据牛顿第二定律:μmg=ma,a=μg,滑块B停止滑动的时间t=
| v2 |
| a |
第二阶段:B停止运动后,A继续在车上滑动,设到时刻t2物体A与车有共同速度v,则t2=
| v1-v |
| a |
第三阶段:t2之后,车以速度v做匀速直线运动到t=4.0s为止.
小车运动的速度--时间图线如图所示.
答:(1)A、B在车上都停止滑动时车的速度为0.60m/s,方向向右.
(2)车的长度至少为6.8m.
(3)速度时间图线如图所示.
点评:把动量守恒和能量守恒结合起来求解是常见的问题.此题要求清楚运动过程中能量的转化.以及能够知道小车在整个过程中的运动情况.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
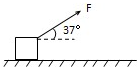 (2011?河南二模)如图所示,质量m=0.78kg的金属块放在水平桌面上,在斜向上的恒定拉力F作用下,向右以v0=2.0m/s的速度作匀速直线运动,已知F=3.0N,方向与水平面之间的夹角θ=37°.(sinθ=0.6,cosθ=0.8,g取10m/s2)
(2011?河南二模)如图所示,质量m=0.78kg的金属块放在水平桌面上,在斜向上的恒定拉力F作用下,向右以v0=2.0m/s的速度作匀速直线运动,已知F=3.0N,方向与水平面之间的夹角θ=37°.(sinθ=0.6,cosθ=0.8,g取10m/s2) 如图所示,质量M=0.2kg的足够长的长板静止在水平地面上,与地面间动摩擦因数μ1=0.1,另一质量m=0.1kg的小滑块以v0=0.9m/s初速滑上长木板,滑块与长木板间动摩擦因数μ2=0.4,求小滑块自滑上长板到最后静止(相对地面)的过程中运动的路程.(可以认为长板与地面间的最大静摩擦力等于滑动摩擦力,g取10m/s2)
如图所示,质量M=0.2kg的足够长的长板静止在水平地面上,与地面间动摩擦因数μ1=0.1,另一质量m=0.1kg的小滑块以v0=0.9m/s初速滑上长木板,滑块与长木板间动摩擦因数μ2=0.4,求小滑块自滑上长板到最后静止(相对地面)的过程中运动的路程.(可以认为长板与地面间的最大静摩擦力等于滑动摩擦力,g取10m/s2)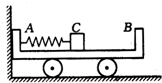 如图所示,质量M=0.8kg的小车静止在光滑的水平面上,左端紧靠竖直墙.在车上左端水平固定着一只弹簧,弹簧右端放一个质量m=0.2kg的滑块,弹簧为原长时,滑块位于C处(滑块可以视为质点),车的上表面AC部分为光滑水平面,CB部分为粗糙水平面.CB长l=1m、与滑块的摩擦因数μ=0.4.水平向左推动滑块,将弹簧压缩,然后再把滑块从静止释放,在压缩弹簧过程中推力做功2.5J,滑块释放后将在车上往复运动,最终停在车上某处.设滑块与车的B端碰撞时机械能无
如图所示,质量M=0.8kg的小车静止在光滑的水平面上,左端紧靠竖直墙.在车上左端水平固定着一只弹簧,弹簧右端放一个质量m=0.2kg的滑块,弹簧为原长时,滑块位于C处(滑块可以视为质点),车的上表面AC部分为光滑水平面,CB部分为粗糙水平面.CB长l=1m、与滑块的摩擦因数μ=0.4.水平向左推动滑块,将弹簧压缩,然后再把滑块从静止释放,在压缩弹簧过程中推力做功2.5J,滑块释放后将在车上往复运动,最终停在车上某处.设滑块与车的B端碰撞时机械能无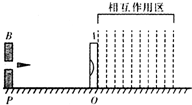 如图所示:质量M=0.40kg的靶盒A位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中划虚线部分所示,当靶盒A进入相互作用区时便受指向O点的恒力F=20N作用,P处有一固定的发射器B,它可根据需要瞄准靶盒并每次发射一颗水平速度υ0=50m/s、质量m=0.10kg的子弹,当子弹打入靶盒A后,便留在盒内,碰撞时间极短.现约定,每当靶盒A停在或到达O点时,都有一颗子弹进入靶盒A内.
如图所示:质量M=0.40kg的靶盒A位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中划虚线部分所示,当靶盒A进入相互作用区时便受指向O点的恒力F=20N作用,P处有一固定的发射器B,它可根据需要瞄准靶盒并每次发射一颗水平速度υ0=50m/s、质量m=0.10kg的子弹,当子弹打入靶盒A后,便留在盒内,碰撞时间极短.现约定,每当靶盒A停在或到达O点时,都有一颗子弹进入靶盒A内.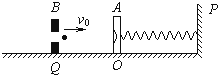 如图所示,质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点,水平轻质弹簧一端栓在固定挡板P上,另一端与靶盒A连接,Q处有一固定的发射器B,它可以瞄准靶盒发射一颗水平速度为v0=50m/s,质量m=0.010kg的弹丸,当弹丸打入靶盒A后,便留在盒内,碰撞时间极短,不计空气阻力,求
如图所示,质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点,水平轻质弹簧一端栓在固定挡板P上,另一端与靶盒A连接,Q处有一固定的发射器B,它可以瞄准靶盒发射一颗水平速度为v0=50m/s,质量m=0.010kg的弹丸,当弹丸打入靶盒A后,便留在盒内,碰撞时间极短,不计空气阻力,求