题目内容
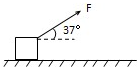（2011?河南二模）如图所示，质量m=0.78kg的金属块放在水平桌面上，在斜向上的恒定拉力F作用下，向右以v0=2.0m/s的速度作匀速直线运动，已知F=3.0N，方向与水平面之间的夹角θ=37°．（sinθ=0.6，cosθ=0.8，g取10m/s2）（1）求金属块与桌面间的动摩擦因数?；
（2）如果从某时刻起撤去拉力F，求撤去拉力后金属块还能在桌面上滑行的最大距离s．
分析：（1）金属块受到重力mg、拉力F、地面的支持力和滑动摩擦力作用，根据力平衡条件和滑动摩擦力公式求出求出μ．
（2）撤去拉力，金属块水平方向受到滑动摩擦力作用而做匀减速运动，要根据牛顿第二定律求出加速度，再根据速度公式求出时间．
（2）撤去拉力，金属块水平方向受到滑动摩擦力作用而做匀减速运动，要根据牛顿第二定律求出加速度，再根据速度公式求出时间．
解答：解：（1）设在拉力作用下金属块所受地面的支持力为N，滑动摩擦力为f，则根据平衡条件得
Fcos37°=f
Fsin37°+N=mg
又f=μN
联立解得μ=0.4
（2）撤去拉力F后，金属块受到滑动摩擦力f′=μmg
根据牛顿第二定律，得加速度大小为a=
=μg=4m/s2
则撤去F后金属块还能滑行的位移为
s=
=
m=0.5m
答：（1）金属块与桌面间的动摩擦因数?为0.4；
（2）撤去拉力后金属块还能在桌面上滑行的最大距离s为0.5m．
Fcos37°=f
Fsin37°+N=mg
又f=μN
联立解得μ=0.4
（2）撤去拉力F后，金属块受到滑动摩擦力f′=μmg
根据牛顿第二定律，得加速度大小为a=
| f′ |
| m |
则撤去F后金属块还能滑行的位移为
s=
| v2 |
| 2a |
| 4 |
| 8 |
答：（1）金属块与桌面间的动摩擦因数?为0.4；
（2）撤去拉力后金属块还能在桌面上滑行的最大距离s为0.5m．
点评：本题是牛顿第二定律和力平衡条件的简单综合，要防止产生这样的错误解答：在拉力F作用时f=μmg．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
（2011?河南二模）某静电场中的电场线如图所示，带电粒子在电场中仅受电场力作用，其运动轨迹如图中虚线所示，由M运动到N，以下说法正确的是（ ）
（2011?河南二模）如图所示，半径R=0.4m的光滑半圆轨道与粗糙的水平面相切于A点，质量为m=1kg的小物体（可视为质点）在水平拉力F的作用下，从静止开始由C点运动到A点，物体从A点进入半圆轨道的同时撤去外力F，物体沿半圆轨道通过最高点B后做平抛运动，正好落在C点，已知xAC=2m，F=15N，g取10m/s2，试求：
（2011?河南二模）如图所示，平行板电容器的两极板A、B与电池两极相连，一带正电小球悬挂在电容器内部．闭合开关S，电容器充电完毕后悬线偏离竖直方向的夹角为θ，则（ ）
（2011?河南二模）为了让乘客乘车更为舒适，某探究小组设计了一种新的交通工具，乘客的座椅能随着坡度的变化而自动调整，使座椅始终保持水平，如图所示．当此车减速上坡时，乘客（ ）