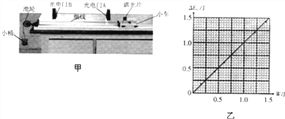
题目内容
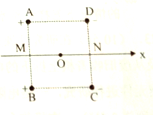
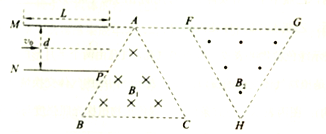
【题目】如图所示，两块平行金属极板MN水平放置，板长L=1m、间距
，两金属板间电压
；在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域，正三角形ABC内存在垂直纸面向里的匀强磁场
，三角形的上顶点A与上金属板M平齐，BC边与金属板平行，AB边的中点P恰好在下金属板N的右端点；正三角形FGH内存在垂直纸面向外的匀强 磁场
，已知A、F、G处于同一直线上，B、C、H也处于同一直线上，AF两点距离为
。现从平行金属极板MN左端沿中心轴线方向入射一个重力不计的带电粒子，若粒子的质量为
，带电量为
，初速度为
，
（1）求该粒子从电场中射出时的速度v的大小和方向；
（2）若该粒子进入中间三角形区域后从AC边界垂直射出，求该区域的磁感应强度
；
（3）若使该粒子由FH边界进入FGH区域并能再次回到FH边界，求
应满足的条件。
【答案】（1）
，垂直于AB方向出射 （2）
(3) 
【解析】试题分析: （1）带电粒子在电场中做类平抛运动，根据平抛运动的基本规律即可求解；（2）求出带电粒子出电场时竖直方向的偏转的位移，根据几何关系及向心力公式即可求解磁场强度；（3）分析知当轨迹与边界GH相切时，对应磁感应强度B2最大，画出粒子运动轨迹根据几何关系及向心力公式即可求解磁场强度应满足的条件．
（1）设带电粒子在电场中做类平抛运动时间t，根据类平抛运动的规律得：
水平方向做匀速运动，则有： 
，解得： 
竖直方向做匀加速运动，则粒子的加速度
竖直方向速度为： 
则粒子射出的速度为： 
设速度v与水平方向夹角为
，则有： 
解得： 
，即垂直于AB方向射出
（2）作出带电粒子的运动轨迹图如图所示：
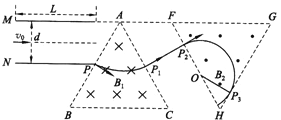
则带电粒子射出电场时数值方向偏移的位移： 
，即粒子由P点垂直AB射入磁场
由几何关系知，在磁场ABC区域内做匀速圆周运动的半径： 
由牛顿第二定律得： 
，解得： 
（3）当轨迹与边界GH相切时，对应磁感应强度
最大，运动轨迹如图所示：
由几何关系可知： 
，解得： 
牛顿第二定律得： 
，解得： 
所以
