题目内容
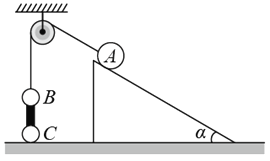
【题目】如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A的质量为4m,B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面,不计空气阻力,在这一过程中A始终在斜面上,下列说法正确的是
A.释放A的瞬间,B的加速度为0.4g
B.C恰好离开地面时,A达到的最大速度为![]()
C.斜面倾角α=45°
D.从释放A到C刚离开地面的过程中,A、B两小球组成的系统机械能守恒
【答案】AB
【解析】
试题分析:设当物体C刚刚离开地面时,弹簧的伸长量为xC,则kxC=mg ①
物体C刚刚离开地面时,以B为研究对象,物体B受到重力mg、弹簧的弹力kxC、细线的拉力T三个力的作用,设物体B的加速度为a,根据牛顿第二定律,
对B有:T-mg-kxC=ma ②
对A有:4mgsinα-T=4ma ③
由②、③两式得
4mgsinα-mg-kxC=5ma ④
当B获得最大速度时,有 a=0 ⑤
由①④⑤式联立,解得 sinα=![]() ,所以:α=30°,故C错误;释放A的瞬间,此时对AB整体加速度大小相同,根据牛顿定律
,所以:α=30°,故C错误;释放A的瞬间,此时对AB整体加速度大小相同,根据牛顿定律![]() B的加速度为0.4g,选项A正确;设开始时弹簧的压缩量xB,则 kxB=mg
B的加速度为0.4g,选项A正确;设开始时弹簧的压缩量xB,则 kxB=mg
设当物体C刚刚离开地面时,弹簧的伸长量为xC,则 kxC=mg
当物体C刚离开地面时,物体B上升的距离以及物体A沿斜面下滑的距离均为: h=xC+xB
由于弹簧处于压缩状态和伸长状态时的弹性势能相等,且物体C刚刚离开地面时,A、B两物体的速度相等,设为vBm,以A、B及弹簧组成的系统为研究对象,由机械能守恒定律得:4mghsinα-mgh=![]() (4m+m)VBm2 ,代入数据,解得:VBm=
(4m+m)VBm2 ,代入数据,解得:VBm=![]() ,故B正确;从释放A到C刚离开地面的过程中,A、B两小球以及弹簧构成的系统机械能守恒,A、B两小球组成的系统机械能不守恒.故D错误;
,故B正确;从释放A到C刚离开地面的过程中,A、B两小球以及弹簧构成的系统机械能守恒,A、B两小球组成的系统机械能不守恒.故D错误;
故选:AB