��Ŀ����
����Ŀ����ͼ����ʾ��һ�ᵯ�ɵ������������ֱ�Ϊm1��m2�������A��B�����ӣ�����ֹ�ڹ⻬��ˮƽ���ϡ���ʹB˲ʱ���ˮƽ���ҵ��ٶ�3m/s���Դ˿�Ϊ��ʱ��㣬�������ٶ���ʱ��仯�Ĺ�����ͼ����ʾ����ͼ����Ϣ�ɵ�(����)
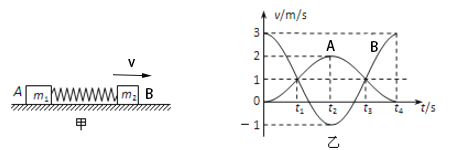
A. ��t1��t3ʱ�������ﵽ��ͬ�ٶ�1m/s,�ҵ��ɶ������쳤״̬
B. ��t3��t4ʱ�̵�����ѹ��״̬�ָ���ԭ��
C. �����������֮��Ϊm1��m2��1��2
D. ��t2ʱ��A��B�Ķ���֮��ΪEk1��Ek2��8��1
���𰸡�BD
����������ͼʾͼ���֪����0��![]() �Ĺ����У�A���ٶ�����B���ٶȼ�С�����ɱ����죬��
�Ĺ����У�A���ٶ�����B���ٶȼ�С�����ɱ����죬��![]() ʱ�������ﵽ��ͬ�ٶ�1m/s����ʱ���ɴ����쳤״̬����
ʱ�������ﵽ��ͬ�ٶ�1m/s����ʱ���ɴ����쳤״̬����![]() ��
��![]() ���̣�A���ٶȼ�������B���ٶȼ�����С�����ɿ�ʼ����������
���̣�A���ٶȼ�������B���ٶȼ�����С�����ɿ�ʼ����������![]() ʱ�̣�A���ٶ����B���ٶ���С�����ɻָ�ԭ������
ʱ�̣�A���ٶ����B���ٶ���С�����ɻָ�ԭ������![]() ��
��![]() ���̣�A���ٶȼ�С��B���ٶ������ɱ�ѹ������
���̣�A���ٶȼ�С��B���ٶ������ɱ�ѹ������![]() ʱ�̣�A��B���ٶ���ȣ�Ϊ1m/s����ʱ���ɵ�ѹ�������
ʱ�̣�A��B���ٶ���ȣ�Ϊ1m/s����ʱ���ɵ�ѹ�������![]() ��
��![]() ���̣�A���ٶȼ�С��B���ٶ����ù��̵��ɻָ�ԭ������
���̣�A���ٶȼ�С��B���ٶ����ù��̵��ɻָ�ԭ������![]() ʱ�̣�B���ٶȵ��ڳ��ٶȣ�A���ٶ�Ϊ�㣬���ɻָ�ԭ���������Ϸ�����֪��A����B��ȷ��ϵͳ�����غ㣬��B�ij��ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�t=0ʱ�̺�
ʱ�̣�B���ٶȵ��ڳ��ٶȣ�A���ٶ�Ϊ�㣬���ɻָ�ԭ���������Ϸ�����֪��A����B��ȷ��ϵͳ�����غ㣬��B�ij��ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�t=0ʱ�̺�![]() ʱ��ϵͳ�ܶ�����ȣ��У�
ʱ��ϵͳ�ܶ�����ȣ��У� ![]() �����
�����![]() ����C������ͼʾͼ���֪����
����C������ͼʾͼ���֪����![]() ʱ��A��B�������ٶȷֱ�Ϊ
ʱ��A��B�������ٶȷֱ�Ϊ![]() ������Ķ���
������Ķ���![]() ����A��B�����Ķ���֮��Ϊ
����A��B�����Ķ���֮��Ϊ![]() ����D��ȷ��
����D��ȷ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�