题目内容
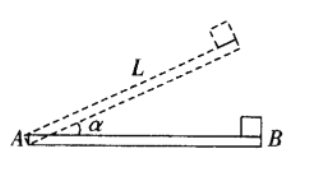
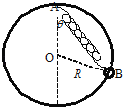
【题目】如图所示,一个所受重力为G的小环套在竖直放置的半径为R的光滑大环上.一轻质弹簧的自然长度为L(L<2R),其一端固定在大圆环的顶点A,另一端与小环相连,当弹簧劲度系数k=k0时,环静止平衡时位于大环上的B点,此时弹簧与竖直方向的夹角θ满足关系式cosθ=![]() .当k取不同值时,弹簧与竖直方向的夹角θ、弹簧弹性力及大环对小环的正压力如何变化?
.当k取不同值时,弹簧与竖直方向的夹角θ、弹簧弹性力及大环对小环的正压力如何变化?
【答案】当![]() =1时,cosθ=1,θ=0,对应的k′=
=1时,cosθ=1,θ=0,对应的k′=![]() ,弹性力达到最大,最大值为2G.
,弹性力达到最大,最大值为2G.
k继续减小,弹性力继续减小,k′≥k≥k″=![]() 时,弹性力在区间(2G≥F≥G),在这过程中G≥N≥0,
时,弹性力在区间(2G≥F≥G),在这过程中G≥N≥0,
k<k″时,N方向转为向上,值不断增加,F继续减小,满足k(2R﹣L)+N=G.
【解析】
以小球为研究对象,则小球受到重力、弹簧的弹力和大环的弹力,小球处于平衡状态,所以受到的三个力的矢量合成关系如图:
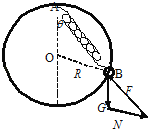
由相似三角形关系,则:![]() =
=![]() ,cosθ=
,cosθ=![]() ,
,
所以:F=2G cosθ=![]() .
.
又:![]() =
=![]() ,N=G,k0减小时,θ减小,F增大,N不变,
,N=G,k0减小时,θ减小,F增大,N不变,
当![]() =1时,cosθ=1,θ=0,对应的k′=
=1时,cosθ=1,θ=0,对应的k′=![]() ,弹性力达到最大,最大值为2G.
,弹性力达到最大,最大值为2G.
k继续减小,θ保持为0,弹簧伸长量不变,但k减小,弹性力继续减小,k′≥k≥k″=![]() 时(对应于k″(2R﹣L)=G),弹性力在区间(2G≥F≥G),在这过程中G≥N≥0,k<k″时,N方向转为向上,值不断增加,F继续减小,满足k(2R﹣L)+N=G
时(对应于k″(2R﹣L)=G),弹性力在区间(2G≥F≥G),在这过程中G≥N≥0,k<k″时,N方向转为向上,值不断增加,F继续减小,满足k(2R﹣L)+N=G

练习册系列答案
相关题目