题目内容
4. 2014年9月24日,“曼加里安”号火星探测器成功进入火星轨道(如图),印度成为了亚洲第一个实现火星探测的国家.假设“曼加里安”号探测器围绕火星做匀速圆周运动,它距火星表面高度为h,运行周期为T,火星的半径为R,则( )
2014年9月24日,“曼加里安”号火星探测器成功进入火星轨道(如图),印度成为了亚洲第一个实现火星探测的国家.假设“曼加里安”号探测器围绕火星做匀速圆周运动,它距火星表面高度为h,运行周期为T,火星的半径为R,则( )| A. | “曼加里安”号探测器运行时的向心加速度为$\frac{4{π}^{2}R}{{T}^{2}}$ | |
| B. | 物体在火星表面自由下落的加速度为$\frac{4{π}^{2}R}{{T}^{2}}$ | |
| C. | “曼加里安”号探测器运行时的线速度为$\frac{2πR}{T}$ | |
| D. | 火星的第一宇宙速度为$\frac{2π\sqrt{R(R+h)^{3}}}{TR}$ |
分析 航天器在火星表面附近绕火星做匀速圆周运动时,由火星的万有引力提供向心力,根据万有引力定律和向心力公式可列出含速率的方程;再研究近地的速度与地球质量的关系,联立即可求解.
解答 解:A、航天器在火星表面附近绕火星做匀速圆周运动时,由火星的万有引力提供向心力,则有:$a={ω}^{2}(R+h)=\frac{4{π}^{2}}{{T}^{2}}(R+h)$.故A错误;
B、由万有引力提供向心力,则$\frac{GMm}{{(R+h)}^{2}}=\frac{m•4{π}^{2}(R+h)}{{T}^{2}}$,在火星的表面:a=$\frac{GM}{{R}^{2}}=\frac{4{π}^{2}{(R+h)}^{3}}{{{R}^{2}T}^{2}}$.故B错误;
C、“曼加里安”号探测器运行时的线速度为v=$\frac{2π(R+h)}{T}$.故C错误;
D、火星的第一宇宙速度为v=$\sqrt{\frac{GM}{R}}$=$\frac{2π\sqrt{R(R+h)^{3}}}{TR}$.故D正确.
故选:D.
点评 对于卫星类型,关键建立卫星运动的模型,理清其向心力来源:万有引力,根据万有引力等于向心力进行解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.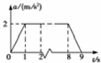 某电梯公寓的电梯在t=0时由静止开始上升,如图所示为电梯运动的加速度-时间图象(选电梯向上运动的方向为正方向),电梯内乘客的质量m=40kg,忽略电梯受到的空气阻力和其他摩擦阻力,向上运行的动力只有竖直向上的电动机的拉力,重力加速度g=10m/s2.下列说法正确的是( )
某电梯公寓的电梯在t=0时由静止开始上升,如图所示为电梯运动的加速度-时间图象(选电梯向上运动的方向为正方向),电梯内乘客的质量m=40kg,忽略电梯受到的空气阻力和其他摩擦阻力,向上运行的动力只有竖直向上的电动机的拉力,重力加速度g=10m/s2.下列说法正确的是( )
 某电梯公寓的电梯在t=0时由静止开始上升,如图所示为电梯运动的加速度-时间图象(选电梯向上运动的方向为正方向),电梯内乘客的质量m=40kg,忽略电梯受到的空气阻力和其他摩擦阻力,向上运行的动力只有竖直向上的电动机的拉力,重力加速度g=10m/s2.下列说法正确的是( )
某电梯公寓的电梯在t=0时由静止开始上升,如图所示为电梯运动的加速度-时间图象(选电梯向上运动的方向为正方向),电梯内乘客的质量m=40kg,忽略电梯受到的空气阻力和其他摩擦阻力,向上运行的动力只有竖直向上的电动机的拉力,重力加速度g=10m/s2.下列说法正确的是( )| A. | 第9s内乘客处于失重状态 | |
| B. | 1-8s内乘客处于平衡状态 | |
| C. | 第2s内乘客对电梯的压力大小为480N | |
| D. | 第1s内电梯速度的增加量为2m/s |
13. 如图所示,a、b两颗质量相同的人造地球卫星分别在半径不同的轨道上绕地球做匀速圆周运动,下列说法正确的是( )
如图所示,a、b两颗质量相同的人造地球卫星分别在半径不同的轨道上绕地球做匀速圆周运动,下列说法正确的是( )
 如图所示,a、b两颗质量相同的人造地球卫星分别在半径不同的轨道上绕地球做匀速圆周运动,下列说法正确的是( )
如图所示,a、b两颗质量相同的人造地球卫星分别在半径不同的轨道上绕地球做匀速圆周运动,下列说法正确的是( )| A. | 卫星a的线速度大于卫星b的线速度 | B. | 卫星a的周期大于卫星b的周期 | ||
| C. | 卫星a的角速度小于卫星b的角速度 | D. | 卫星a的加速度小于卫星b的加速度 |
 某人用力F=100N的恒力,通过滑轮把物体M拉上斜面,如图所示力F方向恒与斜面成60°,若物体沿斜面运动了1m,那么他做的功是多少?(g取10m/s2)
某人用力F=100N的恒力,通过滑轮把物体M拉上斜面,如图所示力F方向恒与斜面成60°,若物体沿斜面运动了1m,那么他做的功是多少?(g取10m/s2)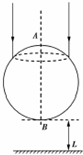 如图所示为一个透明球体的横截面,其半径为R,AB是一竖直直径,现有一束半径为$\frac{\sqrt{3}}{2}$R的圆环形平行细光沿AB方向射向球体(AB所在直径为圆环中心轴线),所有光线经折射后恰好经过B点而在水平光屏上形成一圆亮环,水平光屏到B点的距离为L=R,光在真空中的传播速度为c,求:
如图所示为一个透明球体的横截面,其半径为R,AB是一竖直直径,现有一束半径为$\frac{\sqrt{3}}{2}$R的圆环形平行细光沿AB方向射向球体(AB所在直径为圆环中心轴线),所有光线经折射后恰好经过B点而在水平光屏上形成一圆亮环,水平光屏到B点的距离为L=R,光在真空中的传播速度为c,求: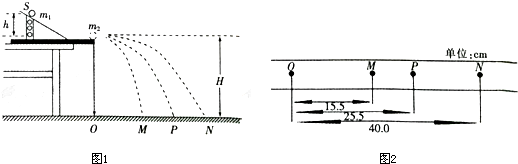
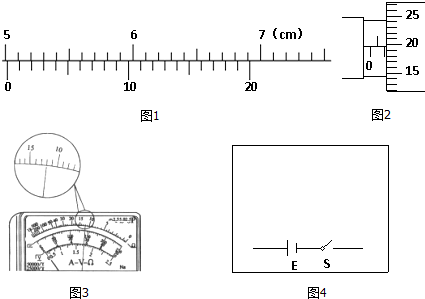
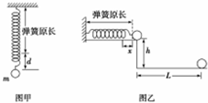 为了“探究动能定理”,查资料得知,弹簧的弹性势能EP=$\frac{1}{2}$kx2,其中k时弹簧的劲度系数,x是弹簧长度的变化量.某同学设想用压缩的弹簧推静止的小球(质量为m)运动来探究这一问题.为了研究方便,把小球放在水平桌面上做实验,让小球在弹力作用下运动,即只有弹簧推力做功.该同学设计实验如下:
为了“探究动能定理”,查资料得知,弹簧的弹性势能EP=$\frac{1}{2}$kx2,其中k时弹簧的劲度系数,x是弹簧长度的变化量.某同学设想用压缩的弹簧推静止的小球(质量为m)运动来探究这一问题.为了研究方便,把小球放在水平桌面上做实验,让小球在弹力作用下运动,即只有弹簧推力做功.该同学设计实验如下: 如图所示,甲、乙两个小孩各乘一辆小车在光滑的水平面上匀速相向行驶.两辆小车速度大小均为v0=4m/s.已知甲所在车上有质量m=1kg的小球若干个,甲和他的车及所带小球的总质量为M1=50kg,乙和他的车的总质量为M2=30kg.为了保证两车不相撞,甲不断地将小球一个一个地以相对地面16m/s的水平速度抛向乙,且被乙接住.假设某一次甲将小球抛出且被乙接住后刚好可保证两车不相撞,试求此时:
如图所示,甲、乙两个小孩各乘一辆小车在光滑的水平面上匀速相向行驶.两辆小车速度大小均为v0=4m/s.已知甲所在车上有质量m=1kg的小球若干个,甲和他的车及所带小球的总质量为M1=50kg,乙和他的车的总质量为M2=30kg.为了保证两车不相撞,甲不断地将小球一个一个地以相对地面16m/s的水平速度抛向乙,且被乙接住.假设某一次甲将小球抛出且被乙接住后刚好可保证两车不相撞,试求此时: