题目内容
15.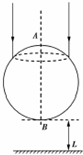 如图所示为一个透明球体的横截面,其半径为R,AB是一竖直直径,现有一束半径为$\frac{\sqrt{3}}{2}$R的圆环形平行细光沿AB方向射向球体(AB所在直径为圆环中心轴线),所有光线经折射后恰好经过B点而在水平光屏上形成一圆亮环,水平光屏到B点的距离为L=R,光在真空中的传播速度为c,求:
如图所示为一个透明球体的横截面,其半径为R,AB是一竖直直径,现有一束半径为$\frac{\sqrt{3}}{2}$R的圆环形平行细光沿AB方向射向球体(AB所在直径为圆环中心轴线),所有光线经折射后恰好经过B点而在水平光屏上形成一圆亮环,水平光屏到B点的距离为L=R,光在真空中的传播速度为c,求:①透明球体的折射率.
②光从入射点传播到光屏所用时间.
分析 ①作出光路图,由几何关系求出入射角和折射角,根据折射定律求解折射率.
②由v=$\frac{c}{n}$求出光在介质中的速度,结合几何关系求出光在圆柱体中运行的位移,从而求出运动的时间.
解答 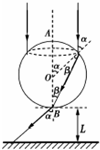 解:①光路图如图所示,则由几何关系知
解:①光路图如图所示,则由几何关系知
Rsinα=$\frac{\sqrt{3}}{2}$R,即α=60°
由图知,α=2β,得β=30°
由折射定律有 n=$\frac{sinα}{sinβ}$=$\sqrt{3}$
②光在介质中的速度为 v=$\frac{c}{n}$
光在透明介质中的传播时间 t1=$\frac{2Rcosβ}{v}$=$\frac{3R}{c}$
由图及折射率定律知光线从B点出射后与竖直方向的夹角为 α=60°
所以光从透明球体出射后到光屏所用时间为 t2=$\frac{2L}{c}$=$\frac{2R}{c}$
所以光从入射点传播到光屏所用时间为 t=t1+t2=$\frac{5R}{c}$
答:
①透明球体的折射率为$\sqrt{3}$.
②光从入射点传播到光屏所用时间是$\frac{5R}{c}$.
点评 解决几何光学问题的关键画出光路图,结合折射定律和几何关系进行求解.

练习册系列答案
相关题目
12.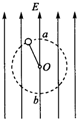 如图所示,在竖直向上的匀强电场中,-根不可伸长的绝缘细绳-端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b.不计空气阻力,则( )
如图所示,在竖直向上的匀强电场中,-根不可伸长的绝缘细绳-端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b.不计空气阻力,则( )
 如图所示,在竖直向上的匀强电场中,-根不可伸长的绝缘细绳-端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b.不计空气阻力,则( )
如图所示,在竖直向上的匀强电场中,-根不可伸长的绝缘细绳-端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b.不计空气阻力,则( )| A. | 小球带负电 | |
| B. | 小球在运动过程中机械能守恒 | |
| C. | 小球在从a点运动到b点的过程中,电势能减小 | |
| D. | 小球在从b点运动到a点的过程中,机械能增大 |
6.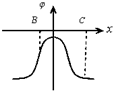 取空间中两等量点电荷的连线为x轴,已知连线上各点电势φ随x变化φ-x图象如图所示,x轴上B、C两点的电场强度分别是EBx、ECx,则下列说法中正确的是( )
取空间中两等量点电荷的连线为x轴,已知连线上各点电势φ随x变化φ-x图象如图所示,x轴上B、C两点的电场强度分别是EBx、ECx,则下列说法中正确的是( )
 取空间中两等量点电荷的连线为x轴,已知连线上各点电势φ随x变化φ-x图象如图所示,x轴上B、C两点的电场强度分别是EBx、ECx,则下列说法中正确的是( )
取空间中两等量点电荷的连线为x轴,已知连线上各点电势φ随x变化φ-x图象如图所示,x轴上B、C两点的电场强度分别是EBx、ECx,则下列说法中正确的是( )| A. | 该静电场由两个等量同种点电荷产生 | |
| B. | 该静电场由两个等量异种点电荷产生 | |
| C. | EBx的大小小于ECx的大小 | |
| D. | 一负电荷沿x轴从B点移到C点的过程中,电势能先增大后减小 |
3. 如图所示,半径为r的圆在竖直平面上,A、B、C、D是圆周上的点,AB水平,CD竖直,在最高点C固定一点电荷,电荷量为-Q,现从A点将一质量为m、电荷量为-q的带电小球(带电小球对点电荷电场的影响忽略不计)由静止释放,该小球沿光滑绝缘轨道ADB运动到D点时的速率为3$\sqrt{gr}$,g为重力加速度,取电场中B点为零电势点,静电力常数为k,则( )
如图所示,半径为r的圆在竖直平面上,A、B、C、D是圆周上的点,AB水平,CD竖直,在最高点C固定一点电荷,电荷量为-Q,现从A点将一质量为m、电荷量为-q的带电小球(带电小球对点电荷电场的影响忽略不计)由静止释放,该小球沿光滑绝缘轨道ADB运动到D点时的速率为3$\sqrt{gr}$,g为重力加速度,取电场中B点为零电势点,静电力常数为k,则( )
 如图所示,半径为r的圆在竖直平面上,A、B、C、D是圆周上的点,AB水平,CD竖直,在最高点C固定一点电荷,电荷量为-Q,现从A点将一质量为m、电荷量为-q的带电小球(带电小球对点电荷电场的影响忽略不计)由静止释放,该小球沿光滑绝缘轨道ADB运动到D点时的速率为3$\sqrt{gr}$,g为重力加速度,取电场中B点为零电势点,静电力常数为k,则( )
如图所示,半径为r的圆在竖直平面上,A、B、C、D是圆周上的点,AB水平,CD竖直,在最高点C固定一点电荷,电荷量为-Q,现从A点将一质量为m、电荷量为-q的带电小球(带电小球对点电荷电场的影响忽略不计)由静止释放,该小球沿光滑绝缘轨道ADB运动到D点时的速率为3$\sqrt{gr}$,g为重力加速度,取电场中B点为零电势点,静电力常数为k,则( )| A. | O点电场强度大小是A点的$\sqrt{2}$倍 | |
| B. | A点电势比D点的高 | |
| C. | 带电小球在D点具有的电势能为-$\frac{7mgr}{2}$ | |
| D. | 带电小球在D点受轨道的作用力为10mg |
20.江苏卫视《最强大脑》曾经播出过吕飞龙用“狮吼功”震碎玻璃杯的表演,该表演引起了众多网友的热议.有关人员在实验室进行了模拟.用手指轻弹一只玻璃杯,可以听到清脆的声音,测得这声音的频率为500Hz,将这只玻璃杯放在一个大功率的声波发声器前,操作人员通过调整其发出的声波,能使玻璃杯碎掉.下列说法中正确的是( )
| A. | 操作人员只要把声波发生器发出的声波频率调到最大 | |
| B. | 操作人员只要把声波发生器输出的功率调到最大 | |
| C. | 操作人员必须同时把声波发生器输出的功率和发出声波的频率调到最大 | |
| D. | 操作人员必须将声波发生器发出的声波频率调到约为500Hz,且适当增大其输出功率 |
7.手机已经是现代人不可缺少的随身物品之一,它是借助电磁波来完成通信工作的.下列说法正确的是( )
| A. | 手机只是一个电磁波发射器,不是接收器 | |
| B. | 手机既是一个电磁波发射器,又是电磁波接收器 | |
| C. | 考场上使用的手机信号屏蔽器是利用静电屏蔽的原理 | |
| D. | 考场上使用的手机信号屏蔽器是通过发射电磁波来干扰手机工作 |
4. 2014年9月24日,“曼加里安”号火星探测器成功进入火星轨道(如图),印度成为了亚洲第一个实现火星探测的国家.假设“曼加里安”号探测器围绕火星做匀速圆周运动,它距火星表面高度为h,运行周期为T,火星的半径为R,则( )
2014年9月24日,“曼加里安”号火星探测器成功进入火星轨道(如图),印度成为了亚洲第一个实现火星探测的国家.假设“曼加里安”号探测器围绕火星做匀速圆周运动,它距火星表面高度为h,运行周期为T,火星的半径为R,则( )
 2014年9月24日,“曼加里安”号火星探测器成功进入火星轨道(如图),印度成为了亚洲第一个实现火星探测的国家.假设“曼加里安”号探测器围绕火星做匀速圆周运动,它距火星表面高度为h,运行周期为T,火星的半径为R,则( )
2014年9月24日,“曼加里安”号火星探测器成功进入火星轨道(如图),印度成为了亚洲第一个实现火星探测的国家.假设“曼加里安”号探测器围绕火星做匀速圆周运动,它距火星表面高度为h,运行周期为T,火星的半径为R,则( )| A. | “曼加里安”号探测器运行时的向心加速度为$\frac{4{π}^{2}R}{{T}^{2}}$ | |
| B. | 物体在火星表面自由下落的加速度为$\frac{4{π}^{2}R}{{T}^{2}}$ | |
| C. | “曼加里安”号探测器运行时的线速度为$\frac{2πR}{T}$ | |
| D. | 火星的第一宇宙速度为$\frac{2π\sqrt{R(R+h)^{3}}}{TR}$ |
 某同学用如图甲所示电路描绘一个“2.8V、1.5W”的小灯泡的伏安特性曲线,并将实验中得到的数据描在图乙所示的I-U坐标系中.
某同学用如图甲所示电路描绘一个“2.8V、1.5W”的小灯泡的伏安特性曲线,并将实验中得到的数据描在图乙所示的I-U坐标系中.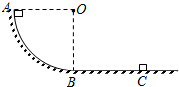 如图所示,AB为四分之一光滑圆弧轨道,半径R=0.8m,BC是水平轨道.物块(可视为质点)从A点由静止开始下滑,物块最终停在水平轨道上C点,若物块与BC间的动摩擦因数μ=0.8,求:
如图所示,AB为四分之一光滑圆弧轨道,半径R=0.8m,BC是水平轨道.物块(可视为质点)从A点由静止开始下滑,物块最终停在水平轨道上C点,若物块与BC间的动摩擦因数μ=0.8,求: