题目内容
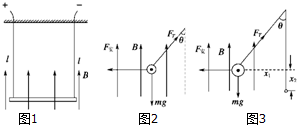
17. 如图所示,导体ab质量为0.2kg,电阻为0.1Ω,跨放在足够长的金属U形框架上,整个框架处在匀强磁场中,磁场方向与框架斜面垂直,框架斜面与水平夹角α=30°,B=2T,框架两平行导轨间距为50cm,导体与导轨间的摩擦及框架电阻忽略不计,取g=10m/s2.求静止导体由高处沿倾斜轨道向下运动过程中:
如图所示,导体ab质量为0.2kg,电阻为0.1Ω,跨放在足够长的金属U形框架上,整个框架处在匀强磁场中,磁场方向与框架斜面垂直,框架斜面与水平夹角α=30°,B=2T,框架两平行导轨间距为50cm,导体与导轨间的摩擦及框架电阻忽略不计,取g=10m/s2.求静止导体由高处沿倾斜轨道向下运动过程中:(1)最大加速度是多少?
(2)最大速度是多少?
(3)当运动速度为最大速度一半时,导体的加速度是多大?此时通过导体的电流强度是多大?
分析 (1)由牛顿第二定律可以求出导体的加速度.
(2)导体匀速运动时速度最大,应用安培力公式与平衡条件可以求出最大速度.
(3)应用牛顿第二定律与E=BLv、欧姆定律求出加速度与电流.
解答 解:导体受力如图所示:
导体ab受到沿斜面向上的安培力FB,并且随其下滑速度增加而增加,则导体ab的最大加速度是其静止的时刻.
(1)由牛顿第二定律得:mgsinα=ma,解得:a=gsinα=5m/s2;
(2)导体匀速运动时速度最大,由平衡条件得:mgsinα=$\frac{{B}^{2}{L}^{2}{v}_{max}}{R}$,
解得:${v_{max}}=\frac{mgRsinα}{{{B^2}{L^2}}}=\frac{0.2×10×0.1×0.5}{{{2^2}×{{0.5}^2}}}=0.1$m/s;
(3)安培力:$F∝v,当v'=\frac{{{v_{max}}}}{2}$,
有mgsinα-$\frac{1}{2}$mgsinα=ma′,所以
加速度:a′=$\frac{1}{2}$gsinα=$\frac{1}{2}$×10×$\frac{1}{2}$=2.5m/s2
电流:$I'=\frac{BLv'}{R}=\frac{2×0.5×0.1}{0.1×2}=0.5$A;
答:(1)最大加速度是5m/s2;
(2)最大速度是0.1m/s;
(3)当运动速度为最大速度一半时,导体的加速度是2.5m/s2,此时通过导体的电流强度是0.5A.
点评 本题考查了分析导体棒的运动情况、求最大速度、求热功率,由安培力公式求出安培力、应用牛顿第二定律、平衡条件、电功率公式即可正确解题.

练习册系列答案
相关题目
10.如图所示,开关闭合后,在滑动变阻器滑片P向右滑动的过程中( )
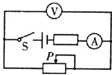

| A. | 电流表示数变小,电压表示数变大 | B. | 电流表示数变小,电压表示数变小 | ||
| C. | 电流表示数变大,电压表示数变大 | D. | 电流表示数变大,电压表示数变小 |
5.我国是世界上能够发射地球同步卫星的少数国家之一,关于同步卫星,正确的说法是( )
| A. | 可以定点在牟平区的上空 | |
| B. | 运动周期与地球自转周期相同的卫星肯定是同步卫星 | |
| C. | 同步卫星内的仪器处于超重状态 | |
| D. | 同步卫星轨道平面与赤道平面重合 |
12.某实验小组利用如图(甲)所示的实验装置来探究当合外力一定时,物体运动的加速度与其质量之间的关系.

(1)由图(甲)中刻度尺读出两个光电门中心之间的距离x=24cm,测得遮光条的宽度d=0.52cm,该实验小组在做实验时,将滑块从图(甲)所示位置由静止释放,由数字计时器可以读出遮光条通过光电门1的时间△t1,遮光条通过光电门2的时间△t2,则滑块经过光电门1时的瞬时速度的表达式v1=$\frac{d}{△{t}_{1}}$,滑块经过光电门2时的瞬时速度的表达式v2=$\frac{d}{△{t}_{2}}$,则滑块的加速度的表达式a=$\frac{{d}^{2}(△{{t}_{1}}^{2}-△{{t}_{2}}^{2})}{2s△{{t}_{1}}^{2}△{{t}_{2}}^{2}}$.(以上表达式均用字母表示)
(2)在本次实验中,实验小组通过改变滑块质量总共做了6组实验,得到如表所示的实验数据,通过分析表中数据后,你得出的结论是加速度随质量的增大而减小
(3)现需通过图象进一步验证你的结论,请利用表格数据,在图(乙)坐标系中描点作出相应图象.

(1)由图(甲)中刻度尺读出两个光电门中心之间的距离x=24cm,测得遮光条的宽度d=0.52cm,该实验小组在做实验时,将滑块从图(甲)所示位置由静止释放,由数字计时器可以读出遮光条通过光电门1的时间△t1,遮光条通过光电门2的时间△t2,则滑块经过光电门1时的瞬时速度的表达式v1=$\frac{d}{△{t}_{1}}$,滑块经过光电门2时的瞬时速度的表达式v2=$\frac{d}{△{t}_{2}}$,则滑块的加速度的表达式a=$\frac{{d}^{2}(△{{t}_{1}}^{2}-△{{t}_{2}}^{2})}{2s△{{t}_{1}}^{2}△{{t}_{2}}^{2}}$.(以上表达式均用字母表示)
(2)在本次实验中,实验小组通过改变滑块质量总共做了6组实验,得到如表所示的实验数据,通过分析表中数据后,你得出的结论是加速度随质量的增大而减小
| m(g) | a(m/s2) |
| 250 | 2.02 |
| 300 | 1.65 |
| 350 | 1.33 |
| 400 | 1.25 |
| 500 | 1.00 |
| 800 | 0.63 |
6.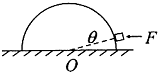 在竖直平面内有一半圆形光滑轨道固定在水平面上,O为半圆轨道的圆心,一质量为m的小滑块,在水平力F的作用下从图示位置开始,缓慢向最高点移动.设滑块所受支持力为FN,则在移动过程中,下列判断正确的是( )
在竖直平面内有一半圆形光滑轨道固定在水平面上,O为半圆轨道的圆心,一质量为m的小滑块,在水平力F的作用下从图示位置开始,缓慢向最高点移动.设滑块所受支持力为FN,则在移动过程中,下列判断正确的是( )
 在竖直平面内有一半圆形光滑轨道固定在水平面上,O为半圆轨道的圆心,一质量为m的小滑块,在水平力F的作用下从图示位置开始,缓慢向最高点移动.设滑块所受支持力为FN,则在移动过程中,下列判断正确的是( )
在竖直平面内有一半圆形光滑轨道固定在水平面上,O为半圆轨道的圆心,一质量为m的小滑块,在水平力F的作用下从图示位置开始,缓慢向最高点移动.设滑块所受支持力为FN,则在移动过程中,下列判断正确的是( )| A. | F缓慢增大 | B. | F保持不变 | C. | FN保持不变 | D. | FN缓慢减小 |
7.甲、乙、丙三辆汽车同时以相同的速度经过某一路标,此后甲一直做匀速直线运动;乙先加速后减速;丙先减速后加速,它们经过下一个路标时的速度仍相同,则( )
| A. | 甲车先经过下一个路标 | B. | 乙车先经过下一个路标 | ||
| C. | 丙车先经过下一个路标 | D. | 无法判断谁先经过下一路标 |