题目内容
2.如图甲所示,电荷量为q=1×10-4C的带正电的小物块置于绝缘水平面上,所在空间存在方向沿水平向右的电场,电场强度E的大小与时间的关系如图乙所示,物块运动速度与时间t的关系如图丙所示,取重力加速度g=10m/s2.求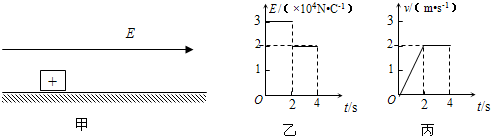
(1)前2秒内电场力做的功;
(2)物块的质量;
(3)物块与水平面间的动摩擦因数.
分析 (1)根据速度时间图线求出匀加速运动的加速度,得出匀加速运动的位移,根据电场力和位移求出前2s内电场力做功的大小.
(2、3)根据物块做匀速运动得出电场力和摩擦力相等,求出摩擦力的大小,对匀加速运动运用牛顿第二定律求出物块的质量和动摩擦因数的大小.
解答 解:(1)由图象可知,在前两秒内
a=$\frac{2}{2}m/{s}^{2}$=1m/s2
S=$\frac{1}{2}$at2=$\frac{1}{2}×1×4m$=2m
W=qE1S=1×10-4×3×104×2J=6J
(2、3)后两秒物体做匀速运动
E2q=μmg
前两秒做匀加速运动
E2q-E1q=ma
代入数据解得:m=1kg,μ=0.2.
答:(1)前2秒内电场力做的功为6J;
(2)物块的质量为1kg;
(3)物块与水平面间的动摩擦因数为0.2.
点评 本题考查了牛顿第二定律和速度时间图线的综合运用,抓住匀速运动时,电场力和摩擦力相等,然后结合匀加速运动过程运用牛顿第二定律求解,难度中等.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
10.关于电功W和电热Q的说法,正确的是( )
| A. | 在任何电路里都有W=UIt,Q=I2Rt,且W=Q | |
| B. | 在任何电路里都有W=UIt,Q=UIt,且W不一定等于Q | |
| C. | W=UIt,Q=I2Rt均只在纯电阻电路中才成立 | |
| D. | W=UIt在任何电路中都成立,W=I2Rt求纯电阻消耗的能量时成立 |
7.有两个共点力F1、F2,其中F1=6N,F2=9N,则它们的合力大小不可能是( )
| A. | 18N | B. | 11N | C. | 5N | D. | 2N |
14.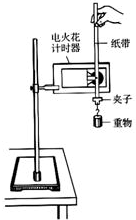 在验证机械能守恒定律的实验中,要验证的是重物重力势能的减少量等于它动能的增加量.以下是实验操作的一些步骤,将没有必要的步骤挑选出来( )
在验证机械能守恒定律的实验中,要验证的是重物重力势能的减少量等于它动能的增加量.以下是实验操作的一些步骤,将没有必要的步骤挑选出来( )
 在验证机械能守恒定律的实验中,要验证的是重物重力势能的减少量等于它动能的增加量.以下是实验操作的一些步骤,将没有必要的步骤挑选出来( )
在验证机械能守恒定律的实验中,要验证的是重物重力势能的减少量等于它动能的增加量.以下是实验操作的一些步骤,将没有必要的步骤挑选出来( )| A. | 把打点计时器固定在铁架台上,并用导线把它和交流电源连接起来 | |
| B. | 用天平称出重锤的质量 | |
| C. | 把纸带的一端固定在重锤上,另一端穿过打点计时器的限位孔,把重锤提升到一定的高度 | |
| D. | 接通电源 | |
| E. | 释放纸带 | |
| F. | 用秒表测出重锤下落的时间 | |
| G. | 重复几次,得到3-5条符合要求的纸带 |
11.关于电容器和电容,下列说法正确的是( )
| A. | 电容器所带的电荷越多,电容就越大 | |
| B. | 用电源给电容器充电时,两极板一定带有等量异种电荷 | |
| C. | 如果某一个电容器的带电量为零,那么这个电容器的电容就为零 | |
| D. | 电容器的电容是表征电容器容纳电荷的本领的物理量,它由电容器本身的构造和介质材料决定 |
12.一个质量为2kg的物体,在10个共点力作用下做匀速直线运动.现突然同时撤去大小分别为10N、12N和14N的三个力,其余的力大小方向均保持不变,关于此后该物体运动的说法中正确的是( )
| A. | 可能做匀速直线运动 | |
| B. | 可能做匀变速曲线运动,加速度大小可能是5m/s2 | |
| C. | 可能做匀速圆周运动,向心加速度大小5m/s2 | |
| D. | 可能做匀减速直线运动,加速度大小是20m/s2 |
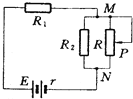 如图所示E=6V,r=0.5Ω,R1=1.5Ω,R2=2Ω,可变电阻器R的最大阻值为2Ω,在滑动片P从最上端滑到最下端的过程中,通过R1的电流的最大值是3A,M、N两点间电压的最大值是2V.
如图所示E=6V,r=0.5Ω,R1=1.5Ω,R2=2Ω,可变电阻器R的最大阻值为2Ω,在滑动片P从最上端滑到最下端的过程中,通过R1的电流的最大值是3A,M、N两点间电压的最大值是2V.
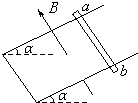 如图所示,导体ab质量为0.2kg,电阻为0.1Ω,跨放在足够长的金属U形框架上,整个框架处在匀强磁场中,磁场方向与框架斜面垂直,框架斜面与水平夹角α=30°,B=2T,框架两平行导轨间距为50cm,导体与导轨间的摩擦及框架电阻忽略不计,取g=10m/s2.求静止导体由高处沿倾斜轨道向下运动过程中:
如图所示,导体ab质量为0.2kg,电阻为0.1Ω,跨放在足够长的金属U形框架上,整个框架处在匀强磁场中,磁场方向与框架斜面垂直,框架斜面与水平夹角α=30°,B=2T,框架两平行导轨间距为50cm,导体与导轨间的摩擦及框架电阻忽略不计,取g=10m/s2.求静止导体由高处沿倾斜轨道向下运动过程中: