题目内容
1. 如图所示,一束截面为圆形(半径R)的平行白光垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形彩色亮区.已知玻璃半球的半径为R,屏幕S至球心的距离为d(d>3R),不考虑光的干涉和衍射,试问:
如图所示,一束截面为圆形(半径R)的平行白光垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形彩色亮区.已知玻璃半球的半径为R,屏幕S至球心的距离为d(d>3R),不考虑光的干涉和衍射,试问:①在屏幕S上形成的圆形亮区的最外侧是什么颜色?
②若玻璃半球对最外侧色光的折射率为n,求出圆形亮区的最大半径.
分析 ①当光线从空气垂直射入半圆玻璃砖,光线不发生改变,当入射角小于临界角时,光线才能再从玻璃砖射出,所以平行白光中的折射率不同,导致临界角不同,因此偏折程度不同,从而确定圆形亮区的最外侧的颜色;
②光线沿直线从O点穿过玻璃,方向不变.从A点射出玻璃砖的光线方向向右偏折,射到屏幕S上圆形亮区,作出光路图,由光的折射定律结合数学几何知识求出圆形亮区的最大半径.
解答  解:①在屏幕S上形成的圆形亮区的最外侧是紫色.
解:①在屏幕S上形成的圆形亮区的最外侧是紫色.
因为当平行光从玻璃中射向空气时,由于紫光的折射率的最大,临界角最小,所以首先发生全反射,因此出射光线与屏幕的交点最远.故圆形亮区的最外侧是紫光.
②如图所示,当光在图中A点沿切线方向射出玻璃时,光线射在屏上最外侧C点,在光屏上形成一个以CD为半径的圆形光斑.
设紫光临界角为C,则图中α=C
由全反射的知识:sinC=$\frac{1}{n}$,
得:sinα=$\frac{1}{n}$
所以有:cosα=$\sqrt{1-si{n}^{2}α}$=$\sqrt{1-\frac{1}{{n}^{2}}}$
tanα=$\frac{sinα}{cosα}$=$\frac{1}{\sqrt{{n}^{2}-1}}$
由几何知识可得:OB=$\frac{R}{cosα}$=$\frac{nR}{\sqrt{{n}^{2}-1}}$
BD=d-OB=d-$\frac{nR}{\sqrt{{n}^{2}-1}}$
CD=$\frac{BD}{tanα}$=$\frac{\sqrt{{n}^{2}-1}d-nR}{\sqrt{{n}^{2}-1}}$
CD即为圆形亮区的最大半径.
答:①在屏幕S上形成的圆形亮区的最外侧是紫色.
②圆形亮区的最大半径为$\frac{\sqrt{{n}^{2}-1}d-nR}{\sqrt{{n}^{2}-1}}$.
点评 本题是几何光学问题,关键是作出光路图,理解形成圆形光斑的原因,要掌握全反射的条件,根据几何知识解题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示为演示气体定律的趣味仪器--哈勃瓶,它是一个瓶颈很短的平底大烧瓶,在瓶内塞有一气球,气球的吹气口反扣在瓶口上.在一次实验中,瓶内在气球和瓶壁之间封闭一定质量的气体,在对气球缓慢吹气的过程中,当瓶内气体体积减小△V时,压强增大20%.若使瓶内气体体积减小3△V,则其压强增大( )
如图所示为演示气体定律的趣味仪器--哈勃瓶,它是一个瓶颈很短的平底大烧瓶,在瓶内塞有一气球,气球的吹气口反扣在瓶口上.在一次实验中,瓶内在气球和瓶壁之间封闭一定质量的气体,在对气球缓慢吹气的过程中,当瓶内气体体积减小△V时,压强增大20%.若使瓶内气体体积减小3△V,则其压强增大( )| A. | 150% | B. | 100% | C. | 60% | D. | 50% |
 如图所示,粗细均匀的绝缘棒组成一边长为L的正方形线框,线框上均匀地分布着正电荷,O是线框的中心,现在线框右侧中点A处取下足够短的带电量为q的一小段,将其沿OA连线向右移动$\frac{L}{2}$的距离到B点处,若线框的其它部分的带电量与电荷分布保持不变,则此时O点的电场强度大小为( )
如图所示,粗细均匀的绝缘棒组成一边长为L的正方形线框,线框上均匀地分布着正电荷,O是线框的中心,现在线框右侧中点A处取下足够短的带电量为q的一小段,将其沿OA连线向右移动$\frac{L}{2}$的距离到B点处,若线框的其它部分的带电量与电荷分布保持不变,则此时O点的电场强度大小为( )| A. | k$\frac{q}{{L}^{2}}$ | B. | k$\frac{3q}{2{L}^{2}}$ | C. | k$\frac{3q}{{L}^{2}}$ | D. | k$\frac{5q}{{L}^{2}}$ |
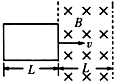 如图所示,矩形线框以恒定速度v自左向右通过有直线边界的匀强磁场,线框宽度等于磁场区域宽度,则在整个过程中,下列说法正确的是( )
如图所示,矩形线框以恒定速度v自左向右通过有直线边界的匀强磁场,线框宽度等于磁场区域宽度,则在整个过程中,下列说法正确的是( )| A. | 线框中的感应电流方向是先逆时针方向,后顺时针方向 | |
| B. | 线框中的感应电流方向是先顺时针方向,后逆时针方向 | |
| C. | 线框进入磁场过程中所受安培力方向向左 | |
| D. | 线框离开磁场过程中所受安培力方向向右 |
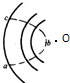 如图所示,一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中虚线abc所示,图中实线是同心圆弧,表示电场的等势面,不计重力,可以判断( )
如图所示,一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中虚线abc所示,图中实线是同心圆弧,表示电场的等势面,不计重力,可以判断( )| A. | 此粒子可能受到静电吸引力的作用 | |
| B. | b点的电势一定大于在a点的电势 | |
| C. | 粒子在a点和c点的速度一定相同 | |
| D. | 粒子在b点的电势能一定大于在a点的电势能 |
 如图所示,两个半径不同而内壁光滑的半圆轨道,固定于地面上,两个相同的小球从与球心同一水平高度上的A、B两点,由静止开始自由下滑,以A点为零势能参考平面,则两球通过轨道最低点时( )
如图所示,两个半径不同而内壁光滑的半圆轨道,固定于地面上,两个相同的小球从与球心同一水平高度上的A、B两点,由静止开始自由下滑,以A点为零势能参考平面,则两球通过轨道最低点时( )| A. | 小球对两轨道的压力不同 | B. | 小球对两轨道的压力相同 | ||
| C. | 小球的机械能不相等 | D. | 小球的机械能相等 |
 如图为一小型电风扇的电路简化图.电机M的线圈电阻为r,理想变压器原、副线圈的匝数 比为n:1,原线圈接电压u=Umsinωt的交流电源.开关S闭合后,电风扇正常运转则( )
如图为一小型电风扇的电路简化图.电机M的线圈电阻为r,理想变压器原、副线圈的匝数 比为n:1,原线圈接电压u=Umsinωt的交流电源.开关S闭合后,电风扇正常运转则( )| A. | 副线圈中交流电频率为$\frac{ω}{2π}$ | B. | 电机两端的电压有效值为$\frac{{U}_{m}}{n}$ | ||
| C. | 通过电机的电流有效值为$\frac{{U}_{m}}{\sqrt{2}nr}$ | D. | 电机的输出功率为$\frac{{{U}_{m}}^{2}}{2{n}^{2}r}$ |
| A. | 英国物理学家卡文迪许用实验的方法测出万有引力常量G | |
| B. | 牛顿应用“理想斜面实验”推翻了亚里士多德的“力是维持物体运动的原因”观点 | |
| C. | 哥白尼创立地心说 | |
| D. | 亚里士多德认为两个从同一高度自由落下的物体,重物体与轻物体下落一样快 |
| A. | 1m/s | B. | 5m/s | C. | 3m/s | D. | 14m/s |