��Ŀ����
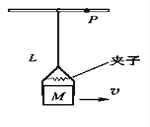
����Ŀ����ͼ��ʾ��һС��鱻���Ӽн�������ͨ������������С���ϣ�С������ˮƽ�⻬ϸ���ϣ��������ΪM����С���ľ���ΪL��������������Ӽ�����Ħ������ΪF.С����������ٶ�v���������˶���С���������ϵĶ���P������ֹͣ��������ϰڶ�.���������У�����ڼ�����û�л���.С���ͼ��ӵ����������ƣ��������ٶ�Ϊg.����˵����ȷ���ǣ�������
A. ������������˶�ʱ�����е���������Mg
B. С����������Pʱ�����е���������2F
C. ������������߶�Ϊ![]()
D. �ٶ�v���ܳ���![]()
���𰸡�AD
��������������������˶�ʱ�������������M������ƽ��״̬����ô���е���������Mg����A��ȷ��С����������Pʱ������M��Բ���˶���������͵��������������ĺ����ṩ��������������е���������Mg������2F��С��ϵ��ȷ������B�������ݻ�е���غ㶨�ɣ���С�Ķ���ת��Ϊ�������ܣ����У�![]() ����������������߶�Ϊ
����������������߶�Ϊ![]() ����C��������Ӷ�����M�����Ħ����Ϊ2F������ţ�ٵڶ����ɣ�������M�����У�
����C��������Ӷ�����M�����Ħ����Ϊ2F������ţ�ٵڶ����ɣ�������M�����У�![]() ����ã�
����ã�![]() �����ٶ�v���ܳ���
�����ٶ�v���ܳ���![]() ����D��ȷ����ѡAD��
����D��ȷ����ѡAD��

��ϰ��ϵ�д�
 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�
�����Ŀ