题目内容
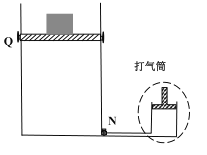
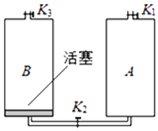
【题目】如图所示,容积均为V的导热气缸A、B下端有细管相连接,阀门K2位于细管的中部。A、B顶部各有一阀门K1、K3,B中有一可自由滑动的活塞(质量、体积均可忽略)。初始时,三个阀门均打开,活塞在B的底部;关闭K2、K3,通过K1给气缸充气,使A中气体的压强达到3p0后关闭K1。已知室温为27℃,大气压强为P0,且保持不变:
(1)打开K2,求稳定时活塞上方气体的体积和压强;
(2)接着打开K3,等活塞稳定后再缓慢加热气缸内气体使其温度升高20℃,求此时活塞下方气体的压强。
【答案】(1)![]() ,2p0;(2)1.6p0
,2p0;(2)1.6p0
【解析】
(1)设打开K2后,稳定时活塞上方气体的压强为p1,体积为V1,依题意,被活塞分开的两部分气体都经历等温过程。由玻意耳定律得
p0V=p1V1
(3p0)V=p1(2V-V1)
联立式得
![]()
p1=2p0
(2)打开K3后,活塞必定上升。设在活塞下方气体与A中气体的体积之和为V2(V2≤2V)时,活塞下方气体压强为p2。由玻意耳定律得
(3p0)V=p2V2
由上式得
![]()
由上式知,打开K3后活塞上升直到B的顶部为止,此时压强为
![]()
设加热后活塞下方气体的压强为p3,气体温度从T1=300K升高到T2=320K的等容过程中,由查理定律得
![]()
将有关数据代入上式得
p3=1.6p0

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目