题目内容
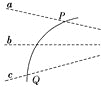
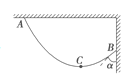
【题目】如图所示,质量为m的匀质细绳,一端系在天花板上的A点,另一端系在竖直墙壁上的B点,平衡后最低点为C点。现测得AC段绳长是CB段绳长的n倍,且绳子B端的切线与墙壁的夹角为α。试求绳子在C处和在A处的弹力分别为多大。(重力加速度为g)
【答案】TC=![]() mgtanα;TA=
mgtanα;TA=![]() mg
mg![]() 。
。
【解析】
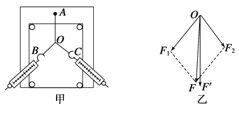
试题以BC段绳子为研究对象,设绳子B端所受弹力为TB,C处所受弹力为TC,如图甲所示。
则在竖直方向上:TBcosα=![]() mg,在水平方向上:TBsinα=TC;
mg,在水平方向上:TBsinα=TC;
联立解之得TC=![]() mgtanα;
mgtanα;
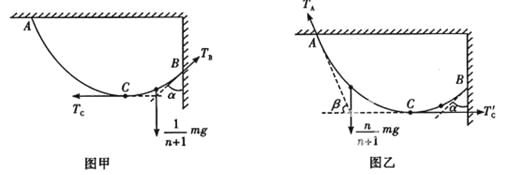
以AC段为研究对象,设绳子A端所受弹力为TA,TA与水平方向的夹角为β,C处所受弹力为TC′,如图乙所示。
则在竖直方向上:TAsinβ=![]() mg,在水平方向上:TAcosβ=TC′;
mg,在水平方向上:TAcosβ=TC′;
而TC= TC′;
联立解之得TA=![]() mg
mg![]() ;
;

练习册系列答案
相关题目