题目内容
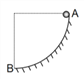
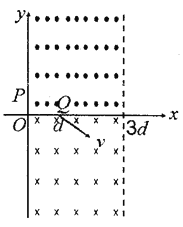
【题目】如图所示，在区域I（0≤
≤3d, y＞0)内存在着垂直XOY平面向外的匀强磁场，磁感应强度大小为B，在区域II (0<x<3d, y<0)内存在着垂直平面向里的匀强磁场，磁感应强度大小为B。质量为m、带电量为q (q>0)的a、b两个粒子同时从y轴上的P点沿x轴正向以不同速率进入区域I。已知某时刻a粒子从Q点(d, 0)进入区域II时，速度方向与x轴正向的夹角为30° (如图），不计粒子的重力和粒子间的相互作用，下列说法正确的是（ ）
A. a粒子在区域I中做圆周运动的半径大小为d
B. 粒子离开区域II时的速度方向沿y轴正方向
C. a粒子在区域I和区域II中运动的总时间为
D. a、b两个粒子一定同时离开磁场
【答案】C
【解析】由几何关系可知，a粒子在区域I中做圆周运动的半径大小为
,选项A错误；粒子进入区域II时，运动的半径与在区域I的运动半径相同，由左手定则可知，粒子向右偏转，由几何关系及对称性可知，粒子从x=3d位置射出，方向与x轴正向成300角，选项B错误；粒子在区域I中做圆周运动的角度为300，在区域II中作圆周运动的角度为600，则总时间为
，选项C正确；b粒子和a粒子的速度不同，则在磁场中运动的轨迹不同，则运动的总时间不同，则两个粒子不可能同时离开磁场，选项D错误；故选C.
练习册系列答案
名校课堂系列答案
相关题目
