题目内容
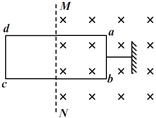
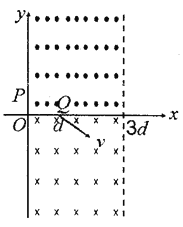
【题目】如图所示,在一倾角为37°的绝缘斜面下端O,固定有垂直于斜面的绝缘挡板.斜面ON段粗糙,长度s=0.02 m,NM段光滑,长度L=0.5 m。在斜面的所在区域有竖直向下的匀强电场,场强为2×105 N/C。有一小滑块质量为2×10-3 kg,带正电,电量为1×10-7 C,小滑块与ON段表面的动摩擦因数为0.75。将小滑块从M点由静止释放,在运动过程中没有电量损失,与挡板相碰后原速返回.已知sin 37°=0.6,cos 37°=0.8,g取10 m/s2。求:

(1)小滑块第一次过N点的速度大小;
(2)小滑块最后停在距离挡板多远的位置;
【答案】(1)![]() (2)x=0.01 m
(2)x=0.01 m
【解析】
试题分析:(1)小滑块第一次过N点的速度为v,
则由动能定理有![]()
代入数据得:![]()
(2)滑块在ON段运动时所受的摩擦力![]()
滑块所受重力、电场力沿斜面的分力![]()
因此滑块沿ON下滑时做匀速运动,上滑时做匀减速运动,速度为零时可停下.
设小滑块与挡板碰撞n次后停在距挡板距离为x处,
则由动能定理得:![]()
由0≤x≤0.02 m,
得:12.5≤n≤13.5
取n=13得:x=0.01 m

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目