题目内容
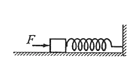
【题目】如图所示，劲度系数为k的轻弹簧的一端固定在墙上，另一端与置于水平面上质量为m的物体A接触，但未与物体A连接，弹簧水平且无形变。现对物体A施加一个水平向右的瞬间冲量，大小为I0，测得物体A向右运动的最大距离为x0，之后物体A被弹簧弹回，最终停在距离初始位置左侧2x0处。已知弹簧始终在弹簧弹性限度内，物体A与水平面间的动摩擦因数为μ，重力加速度为g，下列说法中正确的是：
A.物体A整个运动过程，弹簧对物体A的冲量为零
B.物体A向右运动过程中与弹簧接触的时间一定小于物体A向左运动过程中与弹簧接触的时间
C.物体A向左运动的最大速度
D.物体A与弹簧作用的过程中，系统的最大弹性势能Ep=
【答案】BD
【解析】
A．由于弹簧的弹力一直向左，故弹力的冲量不可能为零；故A错误；
B．物体向右运动过程受向左的弹力和摩擦力，而向左运动过程中受向左的弹力与向右的摩擦力，因此向左运动时的加速度小于向右运动时的加速度；而与弹簧接触向左和向右的位移大小相等，则由位移公式可得，向右运动的时间一定小于向左运动的时间；故B正确；
C．对离开弹簧后再向左运动的x0过程由动能定理可知，
解得离开弹簧时的速度为
而物体在向左运动至弹力与摩擦力相等时速度达最大，故可知向左运动的最大速度一定大于
；故C错误；
D．由动量定理可知I0=mv0；则由功能关系知，系统具有的最大弹性势能
故D正确；
练习册系列答案
应用题作业本系列答案
相关题目
